


Next: Hock and Schittkowski set
Up: Numerical Results of CONDOR.
Previous: Numerical Results of CONDOR.
Contents
We will use for the tests, the following objective function:
![$\displaystyle f(x)= \sum_{i=1}^n \bigg[ a_i - \sum_{j=1}^n ( S_{ij} \sin x_j +
C_{ij} \cos x_j ) \bigg]^2, x \in \Re^n$](img856.png) |
(7.1) |
The way of generating
the parameters of 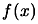 is taken from [RP63], and is as
follows. The elements of the
is taken from [RP63], and is as
follows. The elements of the
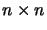 matrices
matrices 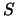 and
and 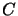 are
random integers from the interval
are
random integers from the interval
![$ [-100 ,\; 100]$](img859.png) , and a vector
, and a vector
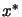 is chosen whose components are random numbers from
is chosen whose components are random numbers from
![$ [-\pi
,\; \pi]$](img860.png) . Then, the parameters
. Then, the parameters
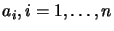 are defined
by the equation
are defined
by the equation 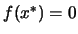 , and the starting vector
, and the starting vector 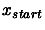 is
formed by adding random perturbations of
is
formed by adding random perturbations of
![$ [-0.1 \pi,\; 0.1 \pi]$](img863.png) to the components of
to the components of 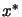 . All distributions of random numbers
are uniform. There are two remarks to do on this objective
function:
. All distributions of random numbers
are uniform. There are two remarks to do on this objective
function:
- Because the number of terms in the sum of squares is equals
to the number of variables, it happens often that the Hessian
matrix
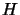 is ill-conditioned around
is ill-conditioned around 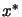 .
.
- Because
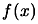 is periodic, it has many saddle points and
maxima.
is periodic, it has many saddle points and
maxima.
Using this test function, it is possible to cover every kind of
problems, (from the easiest one to the most difficult one).
We will compare the CONDOR algorithm with an older algorithm:
''CFSQP''. CFSQP uses line-search techniques. In CFSQP, the
Hessian matrix of the function is reconstructed using a 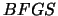 update, the gradient is obtained by finite-differences.
update, the gradient is obtained by finite-differences.
Parameters of CONDOR:
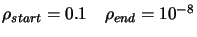 .
.
Parameters of 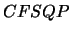 :
:
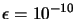 . The algorithm stops
when the step size is smaller than
. The algorithm stops
when the step size is smaller than 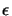 .
.
Recalling that 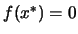 , we will say that we have a success when
the value of the objective function at the final point of the
optimization algorithm is lower then
, we will say that we have a success when
the value of the objective function at the final point of the
optimization algorithm is lower then 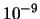 .
.
We obtain the following results, after 100 runs of both
algorithms:
| |
Mean number of |
|
Mean best value of |
Dimension 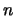 |
function evaluations |
Number of success |
the objective function |
| of the space |
CONDOR |
CFSQP |
CONDOR |
CFSQP |
CONDOR |
CFSQP |
| 3 |
44.96 |
246.19 |
100 |
46 |
3.060873e-017 |
5.787425e-011 |
| 5 |
99.17 |
443.66 |
99 |
27 |
5.193561e-016 |
8.383238e-011 |
| 10 |
411.17 |
991.43 |
100 |
14 |
1.686634e-015 |
1.299753e-010 |
| 20 |
1486.100000 |
-- |
100 |
-- |
3.379322e-016 |
-- |
We can now give an example of execution of the algorithm
to illustrate the discussion of Section 6.2:
Rosenbrock's function (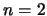 ) ) |
| function evaluations |
Best Value So Far |
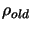 |
| 33 |
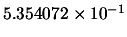 |
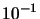 |
| 88 |
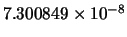 |
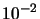 |
| 91 |
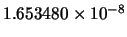 |
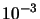 |
| 94 |
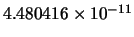 |
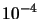 |
| 97 |
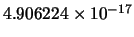 |
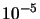 |
| 100 |
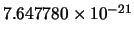 |
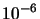 |
| 101 |
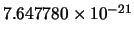 |
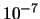 |
| 103 |
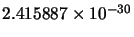 |
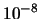 |
With the Rosenbrock's function=
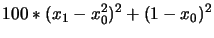
We will use the same choice of parameters (for
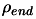 and
and
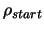 ) as before. The starting point is
) as before. The starting point is
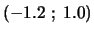 .
.
As you can see, the number of evaluations performed when 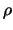 is
reduced is far inferior to
is
reduced is far inferior to
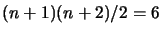 .
.



Next: Hock and Schittkowski set
Up: Numerical Results of CONDOR.
Previous: Numerical Results of CONDOR.
Contents
Frank Vanden Berghen
2004-04-19
![$\displaystyle f(x)= \sum_{i=1}^n \bigg[ a_i - \sum_{j=1}^n ( S_{ij} \sin x_j +
C_{ij} \cos x_j ) \bigg]^2, x \in \Re^n$](img856.png)
![$\displaystyle f(x)= \sum_{i=1}^n \bigg[ a_i - \sum_{j=1}^n ( S_{ij} \sin x_j +
C_{ij} \cos x_j ) \bigg]^2, x \in \Re^n$](img856.png)