


Next: Acknowledgments - Remerciements
Up: Thesis Constrained, non-linear, derivative-free
Previous: Thesis Constrained, non-linear, derivative-free
Contents
This thesis is about parallel, direct and constrained optimization of high-computing-load
objective functions.
The main result is a new original algorithm: CONDOR ('' COnstrained, Non-linear,
Direct, parallel Optimization using trust Region method for high-computing load,
noisy functions''). Other original results are described at the beginning
of Chapter 1. The function of this algorithm
is to find the minimum
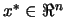 of an objective function
of an objective function
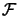
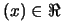 using the least number of function evaluations. It is assumed
that the dominant computing cost of the optimization process is the time needed
to evaluate the objective function
using the least number of function evaluations. It is assumed
that the dominant computing cost of the optimization process is the time needed
to evaluate the objective function
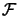
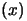 (One evaluation can range from 2 minutes to 2 days). The algorithm
will try to minimize the number of evaluations of
(One evaluation can range from 2 minutes to 2 days). The algorithm
will try to minimize the number of evaluations of
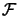 , at the cost of a huge amount of routine work.
, at the cost of a huge amount of routine work.
CONDOR has been designed with one application in mind: the METHOD project. (METHOD
stands for Achievement Of Maximum Efficiency For Process Centrifugal Compressors
THrough New Techniques Of Design). The goal of this project is to optimize the
shape of the blades inside a Centrifugal Compressor (see illustration of the compressor's
blades in Figure 11.1).The objective function
is based on a CFD (computation fluid dynamic) code which simulates the flow of
the gas inside the compressor. The shape of the blades in the compressor is described
by 31 parameters (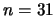 ). We extract from the numerical simulation the outlet pressure,
the outlet velocity, the energy transmit to the gas at stationary conditions.
We aggregate all these indices in one general overall number representing the
quality of the turbine. We are trying to find the optimal set of 31 parameters
for which this quality is maximum. The evaluations of the objective function are
very noisy and often take more than one hour to complete (the CFD code needs time
to ``converge'').
). We extract from the numerical simulation the outlet pressure,
the outlet velocity, the energy transmit to the gas at stationary conditions.
We aggregate all these indices in one general overall number representing the
quality of the turbine. We are trying to find the optimal set of 31 parameters
for which this quality is maximum. The evaluations of the objective function are
very noisy and often take more than one hour to complete (the CFD code needs time
to ``converge'').
CONDOR is a direct optimization tool (i.e., that the derivatives of
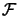 are not required). The only information needed about
the objective function is a simple method (written in Fortran, C++,...) or a program
(a Unix, Windows, Solaris,... executable) which can evaluate the objective function
are not required). The only information needed about
the objective function is a simple method (written in Fortran, C++,...) or a program
(a Unix, Windows, Solaris,... executable) which can evaluate the objective function
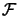
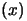 at a given point
at a given point 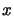 . The algorithm has been specially developed to be very robust against
noise inside the evaluation of the objective function
. The algorithm has been specially developed to be very robust against
noise inside the evaluation of the objective function
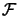
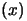 . This situation is very general, the algorithm can thus be applied
on a vast number of situations.
. This situation is very general, the algorithm can thus be applied
on a vast number of situations.
CONDOR is able to use several CPU's in a cluster of computers. Different computer
architectures can be mixed together and used simultaneously to deliver a huge
computing power. The optimizer will make simultaneous evaluations of the objective
function
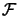
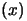 on the available CPU's to speed up the optimization process.
on the available CPU's to speed up the optimization process.
The experimental results are very encouraging and validate the
quality of the approach: CONDOR outperforms many commercial,
high-end optimizer and it might be the fastest optimizer in its
category (fastest in terms of number of function evaluations).
When several CPU's are used, the performances of CONDOR are
unmatched.
The experimental results open wide possibilities in the field of noisy and high-computing-load
objective functions optimization (from two minutes to several days) like, for
instance, industrial shape optimization based on CFD (computation fluid dynamic)
codes (see [CAVDB01,PVdB98,Pol00,PMM$^+$03]) or PDE (partial differential equations)
solvers.
Finally, we propose a new, original, easily comprehensible, free and fully stand-alone
implementation in C/C++ of the optimization algorithm: the CONDOR optimizer. There
is no call to fortran, external, unavailable, expensive, copyrighted libraries.
You can compile the code under Unix, Windows, Solaris,etc. The only library needed
is the standard TCP/IP network transmission library based on sockets (only in
the case of the parallel version of the code).
The algorithms used inside CONDOR are part of the Gradient-Based optimization
family. The algorithms implemented are Dennis-Moré Trust Region steps calculation
(It's a restricted Newton's Step), Sequential Quadratic Programming (SQP), Quadratic
Programming(QP), Second Order Corrections steps (SOC), Constrained Step length
computation using 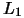 merit function and Wolf condition, Active Set method for active
constraints identification, BFGS update, Multivariate Lagrange Polynomial Interpolation,
Cholesky factorization, QR factorization and more!
merit function and Wolf condition, Active Set method for active
constraints identification, BFGS update, Multivariate Lagrange Polynomial Interpolation,
Cholesky factorization, QR factorization and more!
Many ideas implemented inside CONDOR are from Powell's UOBYQA (Unconstrained Optimization
BY quadratical approximation) [Pow00] for unconstrained, direct optimization.
The main contribution of Powell is Equation 6.6 which
allows to construct a full quadratical model of the objective
function in very few function evaluations (at a low price).
This equation is very successful in that and having a full
quadratical model allows us to reach unmatched convergence speed.
A full comprehension of all the aspects of the
all the algorithms was, for me, one of the most important point. So I started
from scratch and recoded everything. This allowed me to have a fully stand-alone implementation. Full comprehension and full re-implementation
is needed to be able to extend the ideas to the parallel and constrained cases.



Next: Acknowledgments - Remerciements
Up: Thesis Constrained, non-linear, derivative-free
Previous: Thesis Constrained, non-linear, derivative-free
Contents
Frank Vanden Berghen
2004-04-19