CONDOR USER'S GUIDE

\fbox{\begin{minipage}[t]{\textwidth} \begin{center} \huge { Constrained, Non-li... ...igh computing load, noisy objective functions. \par }\end{center}\end{minipage}}

document v1.04

The PDF version of the CONDOR User's Guide v1.05 is available here.

business-insight
I strongly suggest that you read the PDF user's guide (rather than the .html guide) because is the only one that is still updated regularly.
In particular, the PDF guide contains a full documentation about the parallel/distributed version of the condor optimizer.

Contents


Introduction

business-insight
This webpage is a user's guide for CONDOR ``COnstrained, Non-linear, Direct, parallel, multi-objective Optimization using trust Region method for high-computing load, noisy objective functions''. The aim of the CONDOR optimizer is to find the minimum $ x^* \in \Re^n$ of an objective function $ \mbox{$\cal F$}$$ (x) \in \Re$ using the least number of function evaluations. It is assumed that the dominant computing cost of the optimization process is the time needed to evaluate the objective function $ \mbox{$\cal F$}$$ (x)$ (One evaluation can range from 2 minutes to 2 days). The algorithm will try to minimize the number of evaluations of $ \mbox{$\cal F$}$$ (x)$, at the cost of a huge amount of routine work.

CONDOR is mostly useful when used in combination with big software simulators that simulate industrial processes. These kind of simulators are often encountered in the chemical industry (simulators of huge chemical reactors), in the compressor and jet- engine industry (simulators of huge radial turbo-compressors), in the space industry (simulators of the path of a satellite in low orbit around earth),... These simulators were written to allow the design engineer to correctly estimate the consequences of the adjustment of one (or many) design variables (or parameters of the problem). Such softwares very often demands a great deal of computing power. One run of the simulator can take as much as one or two hours to finish. Some extreme simulations take a day to complete.

business-insight
These kind of codes can be used to optimize ``in batch'' the design variables: The research engineer can aggregate the results of the simulation in one unique number which represents the ``goodness'' of the current design (The aggregation process is handled by CONDOR in a specific way that allows to easily do multi-objective optimization). This final number $ y$ can be seen as the result of the evaluation of an objective function $ y=$$ \mbox{$\cal F$}$$ (x)$ where $ x$ is the vector of design variables and $ \mbox{$\cal F$}$ is the simulator. We can run an optimization program which finds $ x^*$: the optimum design: the optimum of $ \mbox{$\cal F$}$$ (x)$.

Here are the assumptions needed to use CONDOR:

CONDOR is able to use several CPU's in a cluster of computers. Different computer architectures can be mixed together and used simultaneously to deliver a huge computing power. The optimizer will make simultaneous evaluations of the objective function $ \mbox{$\cal F$}$$ (x)$ on the available CPU's to speed up the optimization process.

You will never loose one evaluation anymore! Why always throwing away the results of costly evaluations of the objective function? CONDOR manage transparently a database of old evaluations. Using this database, CONDOR is able to ``hot start'' very near the optimum point. This proximity ensure rapid convergence. CONDOR uses the database of old evaluation and a special aggregation process in a way that allows design engineers to easily ``play'' with the different sub-objectives without loosing time. Design engineers can easily customize the objective function, until it finally suits their needs.

The experimental results of CONDOR [VB04] are very encouraging and validates the quality of the approach: CONDOR outperforms many commercial, high-end optimizer and it might be the fastest optimizer in its category (fastest in terms of number of function evaluations). When several CPU's are used, the performances of CONDOR are unmatched. When performing multi-objective optimization, the possibility to ``hot start'' near the optimum point allows to converge to the optimum even faster.

The experimental results open wide possibilities in the field of noisy and high-computing-load objective function optimization (from two minutes to several days) like, for instance, industrial shape optimization based on CFD (computation fluid dynamic) codes (see [CAVDB01,PVdB98,Pol00,PMM$^+$03]) or PDE (partial differential equations) solvers.

More specifically, in the field of aerodynamic shape optimization, optimizers based on genetic algorithm (GA) and Artificial Neural Networks (ANN) are very often encountered. When used on such problems, CONDOR usually outperforms all the state-of-the-art optimizers based on GA and ANN by a factor of 10 to 100 (see [PPGC04] for classical performances of GA+NN optimizer). In brief, CONDOR will converge to the solution of the optimization problem in a time which is 10 to 100 times shorter than any GA+NN optimizers. When the dimension of the search space increases, the performances of optimizers based on GA and ANN are drastically dropping. When using a GA+NN optimizer, a problem with a search-space dimension greater than three is already nearly unsolvable if the objective function is high-computing-load (All what you can expect is a slight improvement of the value of the objective function compared to the value of the objective function at the starting point). Unlike all GA+ANN optimizers, CONDOR scales very well when the search space dimension increases (at least up to 100 dimensions).

CONDOR has been designed with one application in mind: the METHOD project. (METHOD stands for Achievement Of Maximum Efficiency For Process Centrifugal Compressors THrough New Techniques Of Design). The goal of this project is to optimize the shape of the blades inside a Centrifugal Compressor (see illustration of the compressor's blades in Figure 1.1). The objective function is based on a CFD (computation fluid dynamic) code which simulates the flow of the gas inside the compressor. The shape of the blades in the compressor is described by 31 parameters. CONDOR is currently the only optimizer which can solve this kind of problem (an optimizer based on GA+ANN is useless due to the high number of dimensions and the huge computing time needed at each evaluation of the objective function). We extract from the numerical simulation the outlet pressure, the outlet velocity, the energy transmit to the gas at stationary conditions. We aggregate all these indices in one general overall number representing the quality of the turbine. We are trying to find the optimal set of 31 parameters for which this quality is maximum. The evaluations of the objective function are very noisy and often take more than one hour to complete (the CFD code needs time to ``converge'').

Figure 11.1: Illustration of the blades of the compressor
\begin{figure} \centering\epsfig{figure=figures/turbine1.eps, width=7cm, heigh... ....5cm} \epsfig{figure=figures/turbine2.eps, width=7cm, height=6cm} \end{figure}

Finally, The code of CONDOR is completely new, original, easily comprehensible (Object Oriented approach in C++), (partially) free and fully stand-alone. There is no call to fortran, external, unavailable, expensive, copyrighted libraries. You can compile the code under Unix, Windows, Solaris,etc. The only library needed is the standard TCP/IP network transmission library based on sockets (only in the case of the parallel version of the code).

The algorithms used inside CONDOR are part of the Gradient-Based optimization family. The algorithms implemented are Dennis-Moré Trust Region steps calculation (It's a restricted Newton's Step), Sequential Quadratic Programming (SQP), Quadratic Programming(QP), Second Order Corrections steps (SOC), Constrained Step length computation using $ L_1$ merit function and Wolf condition, Active Set method for active constraints identification, BFGS update, Multivariate Lagrange Polynomial Interpolation, Cholesky factorization, QR factorization and more! For more in depth information about the algorithms used, see my thesis [VB04]

Many ideas implemented inside CONDOR are from Powell's UOBYQA (Unconstrained Optimization BY quadratical approximation) [Pow00] for unconstrained, direct optimization. The main contribution of Powell is equation 1.1 which allows to construct a full quadratical model of the objective function in very few function evaluations (at a low price).

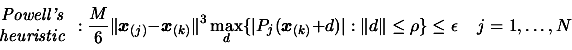\begin{displaymath}\begin{array}{c}\text{\em Powell's} \\ \text{\em heuristic} ... ... \Vert d \Vert \leq \rho \} \leq \epsilon \;\;\;\; j=1,\ldots,N\end{displaymath} (1.1)

See section 3.4.2 (equation 3.37) and section 6.2 (equation 6.6) of [VB04] for a full explanation of this equation. This equation is very successful and having a full quadratical model allows us to reach high convergence speed.

From the user point of view, there are two operating modes available:

  1. XML-Based approach: CONDOR will communicate (using standard ASCII text files) with an external executable which will compute all the evaluations of the objective functions. This approach allows to use very easily old evaluations of the objective function via a database which is internally managed by CONDOR. There is no need to compile or code anything. You give to CONDOR a simple, intuitive configuration file based on XML and CONDOR will start and solve directly your problem! See chapter 2 for a detailed explanation of this approach.
  2. C++ code approach: CONDOR is programmed using Object Oriented approach. Internally, an objective function is represented by an instance of a child of the super-class ``ObjectiveFunction". All you have to do is to create a child of the class ``ObjectiveFunction", instanciate it, and give it to CONDOR. That's all folks!

Formal description

CONDOR is an optimizer for non-linear continuous objective functions subject to box, linear and non-linear constraints. We want to find $ x^* \in$   $ \mbox{$\cal R$}$$ ^n$ which satisfies:

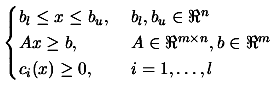$\displaystyle \mbox{$\cal F$}$$\displaystyle (x^*)= \min_x$   $\displaystyle \mbox{$\cal F$}$$\displaystyle (x) \; \;$    Subject to: $\displaystyle \begin{cases}b_l \leq x \leq b_u, \; & b_l,b_u \in \Re^n \\ A x ... ... \Re^{m \times n}, b \in \Re^m \\ c_i(x) \geq 0, \; & i=1,\ldots,l \end{cases}$ (1.2)

Conventions

$ \mbox{$\cal F$}$$ (x): \Re^n \rightarrow \Re$ The objective function. We search for the minimum of it.
$ n$ the dimension of the search space
$ b_l$ and $ b_u$ the box-constraints.
$ A x \geq b$ the linear constraints.
$ c_i(x)$ the non-linear constraints.
$ x^*$ The optimum of $ \mbox{$\cal F$}$$ (x)$. We search for it.
$ k$ The iteration index of the algorithm
$ x_k$ The current point (best point found)
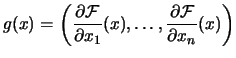$ \displaystyle g(x)= \left( \frac{\partial \mbox{$\cal F$}}{\partial x_1}(x), \ldots, \frac{\partial \mbox{$\cal F$}}{\partial x_n}(x) \right) $ $ g$ is the gradient of $ \cal F$.
$ \displaystyle g_k=g(x_k)$ $ g_k$ is the gradient of $ \mbox{$\cal F$}$ at $ x_k$
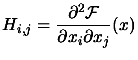$ \displaystyle H_{i,j}=\frac{\partial^2 \mbox{$\cal F$}}{\partial x_i \partial x_j}(x) $ $ H(x)$ is the Hessian matrix of $ \cal F$.
$ H_k=H(x_k)$ The Hessian Matrix of $ \mbox{$\cal F$}$ at point $ x_k$
$ B_k=B(x_k)$ The current approximation of the Hessian Matrix of F at point $ x_k$. If not stated explicitly, we will always assume $ B=H$.
$ H^*=H(x^*)$ The Hessian Matrix at the optimum point.
$ \mbox{$\cal F$}$$ (x_k+\delta ) \approx$   $ \mbox{$\cal Q$}$$ _k(\delta) =$   $ \mbox{$\cal F$}$$ (x_k)+g_k^t \delta+\frac{1}{2}\delta^t B_k \delta$ $ \mbox{$\cal Q$}$$ _k(\delta)$ is the quadratical approximation of $ \mbox{$\cal F$}$ around $ x_k$.



All vectors are column vectors.

An optimization (minimization) algorithm is nearly always based on this simple principle:

  1. Build an approximation (also called ``local model'') of the objective function around the current point.
  2. Find the minimum of this model and move the current point to this minimum. This is called an ``optimization step'' or, in short, a ``step''.
  3. Evaluate the objective function at this new point. Reconstruct the ``local model'' of the objective function around the new point using the new evaluation. Go back to step 2.

Like most optimization algorithms, CONDOR uses, as local model, a polynomial of degree two. There are several techniques to build this quadratic. CONDOR uses multivariate lagrange interpolation technique to build its model. This technique is particularly well-suited when the dimension of the search space is low ($ n<100$).

Let's rewrite this algorithm, using more standard notations:

  1. Build the ``local model'' $ \mbox{$\cal Q$}$$ _k(\delta)$ of the objective function around the current point $ x_k$.
  2. Find the minimum $ \delta_k$ of the local model at $ \mbox{$\cal Q$}$$ _k(x_k+\delta_k)$ and move the current point to this minimum: $ x_{k+1}=x_k+\delta_k$. $ \delta_k$ is the step.
  3. Compute $ y=$$ \mbox{$\cal F$}$$ (x_{k+1})$ and use $ y$ to build the new ``local model'' $ \mbox{$\cal Q$}$$ _{k+1}(\delta)$. Increase k and go back to step 2.

Currently, most of the research in optimization algorithms is oriented to huge dimensional search-space ($ n>1000$). In these algorithms, approximative search directions are computed. CONDOR is one of the very few algorithms which adopts the opposite point of view. CONDOR build the most precise local models of the objective function and computes the most precise steps to reduce at all cost the number of function evaluations.

The material of this chapter is based on the following references: [VB04,Fle87,PT95,BT96,Noc92,CGT99,DS96,CGT00,Pow00].


A basic overview of the CONDOR algorithm.

A (very) basic explanation of the CONDOR algorithm is:

  1. Initialization An initial point $ x_0=x_{start}$, an initial trust region radius $ \Delta_0$ and an initial sampling distance $ \rho_0=\rho_{start}$ are given. In CONDOR, we have $ \Delta_0:=\rho_0$. Let's define $ k$, the iteration index of the algorithm. Set $ k=0$. Let's compute using multivariate interpolation techniques, the initial quadratical approximation of $ \mbox{$\cal F$}$$ (x)$ around $ x_k=x_0=x_{start}$ :
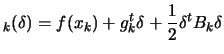
       $\displaystyle \mbox{$\cal Q$}$$\displaystyle _k(\delta) = f(x_k)+ g_k^t \delta + \frac{1}{2} \delta^t B_k \delta $

    The initial sampling points (used to build $ \mbox{$\cal Q$}$$ _k(\delta)$) are separated by a distance of exactly $ \rho _{start}$. Go directly to step 3.
  2. Update the Local Model. Update $ \mbox{$\cal Q$}$$ _k(\delta)$. This will require to ``sample'' the objective function $ \mbox{$\cal F$}$$ (x)$ around the current position $ x_k$ to know what is exactly locally its shape. The sampling points are separated from the current point $ x_k$ by a distance of maximum $ 2 \rho_k$. This update is performed only when we detect that $ \mbox{$\cal Q$}$$ _k(\delta)$ is degenerated and does not represent accurately the real shape of the objective function $ \mbox{$\cal F$}$$ (x)$ anymore.

  3. Step computation Compute a step $ \delta_k$ that goes to the minimum of the local model $ \mbox{$\cal Q$}$$ _k(\delta)$. The length of the steps must be between $ \frac{1}{2} \rho_k$ and $ \Delta_k$. In other words:
    $\displaystyle \mbox{$\cal Q$}$$\displaystyle (\delta_k) = \min_\delta$   $\displaystyle \mbox{$\cal Q$}$$\displaystyle _k(\delta)$    such that $\displaystyle \frac{\rho_k}{2} < \Vert \delta_k \Vert _2 < \Delta_k$ (1.3)
  4. Compute the ``degree of agreement'' $ \tau_k$ between $ \mbox{$\cal F$}$ and $ \mbox{$\cal Q$}$:
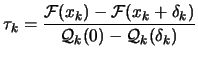    $\displaystyle \tau_k=\frac{\mbox{$\cal F$}(x_k)-\mbox{$\cal F$}(x_k+\delta_k)}{\mbox{$\cal Q$}_k(0)-\mbox{$\cal Q$}_k(\delta_k)}$ (1.4)
  5. update $ x_k$ and $ \Delta_k$, based on $ \tau_k$:
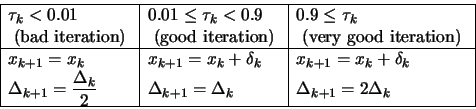    \begin{displaymath}\begin{array}{\vert l\vert l\vert l\vert} \hline \displaystyl... ... & \displaystyle \Delta_{k+1}=2 \Delta_k \\ \hline \end{array}\end{displaymath} (1.5)
  6. Update of $ \rho_k$. If $ \Vert \delta_k \Vert _2 < \rho_k $, the step sizes are becoming small, we are near the optimum, we must increase the precision of $ \mbox{$\cal Q$}$$ _k(\delta)$: decrease $ \rho$.
  7. Increment $ k$. Stop if $ \rho_k=\rho_{end}$ otherwise, go to step 2.

The local model $ \mbox{$\cal Q$}$$ _k$ allows us to compute the steps $ \delta_k$ which we will follow towards the minimum point $ x^*$ of $ \mbox{$\cal F$}$$ (x)$. To which extend can we ``trust'' the local model $ \mbox{$\cal Q$}$? How ``big'' can be the steps $ \delta_k$? The answer is: as big as the Trust Region Radius $ \Delta_k$: We must have $ \Vert \delta_k \Vert< \Delta_k$. $ \Delta_k$ is adjusted dynamically at step 5 of the algorithm. The main idea of step 5 is: only increase $ \Delta_k$ when the local model $ \mbox{$\cal Q$}$$ _k$ reflects well the real function $ \mbox{$\cal F$}$ (and gives us good directions).

Under some very weak assumptions, it can be proven that this algorithm (Trust Region algorithm) is globally convergent to a local optimum [CGT00].

To start the unconstrained version of the CONDOR algorithm, we basically need:

``Fine tuning'' CONDOR parameters

There are only a few parameters which have some influence on the convergence speed of CONDOR. We will review them here.

Initial Sampling distance $ \rho _{start}$


Most people accustomed with finite-difference gradient-based optimization algorithm are confusing the $ \rho _{start}$ or $ \rho_k$ parameters with the $ \epsilon$ parameter used inside the finite difference formula:

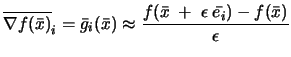
$\displaystyle \displaystyle \overline{\nabla f(\bar{x})}_i = \bar{g}_i(\bar{x}) \approx \frac{f(\bar{x}\;+\;\epsilon \; \bar{e_i})-f(\bar{x})}{\epsilon} $

The $ \rho _{start}$ or $ \rho_k$ parameters are totally different from the $ \epsilon$ parameter. $ \epsilon$ must be chosen as small as possible to accurately approximate the gradient. Contrary to $ \epsilon$, $ \rho _{start}$ should nearly never be taken small.

Recalling from step 1 of the algorithm: ``The initial sampling points are separated by a distance of exactly $ \rho _{start}$''. If $ \rho _{start}$ is too small, we will build a local approximation $ \mbox{$\cal Q$}$$ _k(\delta)$ which will approximate only the noise inside the evaluations of the objective function.



What's happening if we start from a point which is far away from the optimum? CONDOR will make big steps and move rapidly towards the optimum. At each iteration of the algorithm, we must re-construct $ \mbox{$\cal Q$}$$ _k(\delta)$, the quadratic approximation of $ \mbox{$\cal F$}$$ (x)$ around $ x_k$. To re-construct $ \mbox{$\cal Q$}$$ _k(\delta)$ we will use as interpolating points, old evaluations of the objective function. Recalling from step 2 of the algorithm: ``The sampling points are separated from the current point $ x_k$ by a distance of maximum $ 2 \rho_k$''. Thus, if $ x_k$ is moving very fast inside the search space and if $ \rho_k$ is small, we will drop many old sampling points because they are ``too far away''. A sampling point which has been dropped must be replaced by a new one, requiring a costly evaluation of the objective function. $ \rho _{start}$ should thus be chosen big enough to be able to ``move'' rapidly without requiring many evaluations to update/re-construct $ \mbox{$\cal Q$}$$ _k(\delta)$.

$ \rho_k$ represents the average distance between the sample points at iteration $ k$. Above all it represents the ``accuracy'' we want to have when constructing $ \mbox{$\cal Q$}$$ _k(\delta)$. A small $ \rho_k$ will gives us a local model $ \mbox{$\cal Q$}$$ _k(\delta)$ which represents at very high accuracy the local shape of the objective function $ \mbox{$\cal F$}$$ (x)$. Constructing a very accurate approximation of $ \mbox{$\cal F$}$$ (x)$ is very costly (for the reason explained in the previous paragraph). Thus, at the beginning of the optimization process, most of the time, a small $ \rho _{start}$ is a bad idea.


$ \rho _{start}$ can be set to a small value only if we start really close to the optimum point $ x^*$. See section 1.3.3 to know more about this subject.

See also the end of section 1.3.4 to have more insight how to choose an appropriate value for $ \rho _{start}$.


Final Sampling distance $ \rho _{end}$

$ \rho _{end}$ is the stopping criterion. You should stop once you have reached the noise level inside the evaluation of the objective function.


Starting point $ x_{start}$

The closer the starting point $ x_{start}$ is from the optimum point $ x^*$, the better it is.

If $ x_{start}$ is far from $ x^*$, the optimizer may fall into a local minimum of the objective function. The objective function encountered in aero-dynamic shape optimization are in a way ``gentle'': they have usually only one minimum. The difficulty is coming from the noise inside the evaluations of the objective function and from the (long) computing time needed for each evaluation.

Equation 1.3 means that the steps sizes must be greater than $ \frac{1}{2} \rho_k$. Thus, if you start very close to the optimum point $ x^*$ (using for example the hot-start functionality of CONDOR), you should consider to use a very small $ \rho _{start}$ otherwise the algorithm will be forced to make big steps at the beginning of the process. This behavior is easy to identify: it gives a spiraling path to the optimum.


Rescaling factors

From equation 1.3:

$\displaystyle \delta_k = \min_\delta$   $\displaystyle \mbox{$\cal Q$}$$\displaystyle _k(\delta)$    such that $\displaystyle \frac{\rho_k}{2} < \Vert \delta_k \Vert _2 < \Delta_k$

you can see that the step size is maximum $ \Delta_k$ in all the directions/axis of the search space (this is linked to the $ \Vert \: \cdot \: \Vert _2 = L_2$-norm used). This means that the ``trust'' we have inside $ \mbox{$\cal Q$}$$ _k(\delta)$ is spanned over the same distance in all the directions of the search space.



Let's consider the following optimization problem which aims to optimize the shape of the hull of a boat:

   $\displaystyle \mbox{$\cal F$}$$\displaystyle (x^*) = \min_{x \in \Re^2}$   $\displaystyle \mbox{$\cal F$}$$\displaystyle \left( \begin{array}{cl} x_1 = & \text{length of the boat in mm} ... ... (right) at } \\ & \text{ the bow of the boat in radian } \end{array} \right) $

Clearly, $ x_1$ is of magnitude around $ 10^4$ and $ x_2$ is of magnitude around $ 10^1$. Intuitively, it means that we can ``trust'' $ \mbox{$\cal Q$}$$ _k(\delta)$ over a greater distance along the direction $ x_1$ than along direction $ x_2$. It means that we can do ``big'' steps in direction $ x_1$ and ``small'' steps in direction $ x_2$. Unfortunately, without any scaling factors, CONDOR will limit the step size independently of the step direction, preventing to do ``big'' steps in direction $ x_1$ (this is linked to the $ L_2$-norm which is a simple ball instead of an ellipsoid). The aim of the scaling factors is to have all the variable in the same order of magnitude. Let's consider the following equivalent re-scaled optimization problem:

   $\displaystyle \mbox{$\cal F$}$$\displaystyle '(y^*) = \min_{y \in \Re^2}$   $\displaystyle \mbox{$\cal F$}$$\displaystyle ' \left( y_1 ; y_2 \right) = \min_{x \in \Re^2}$   $\displaystyle \mbox{$\cal F$}$$\displaystyle \left( x_1 = 10000 \; y_1 \;\; ; \;\; x_2= 10 \; y_2 \; \right) $

CONDOR will find $ y^*$, the optimum of $ \mbox{$\cal F$}$$ '(y)$ in a shorter time than the time needed to find $ x^*$, the optimum of $ \mbox{$\cal F$}$$ (x)$ because $ \mbox{$\cal F$}$$ '(y)$ is well-scaled (or normalized).

In this example the re-scaling factors are $ r_1=10000$ and $ r_2=10$.

When automatic re-scaling is used, CONDOR will rescale automatically and transparently the variables to obtain the highest speed. The re-scaling factors $ r_i$ are computed in the following way: $ r_i=abs(x_{start,i})+1.0$. If some bounds constrained ($ b_l$ and $ b_u$) are defined on axis $ i$, then $ r_i=b_{u,i}-b_{l,i}$.

To obtain higher convergence speed, you can override the auto-rescaling feature and specify yourself more accurate rescaling factors.

$ \rho _{start}$ and $ \rho _{end}$ are distances expressed in the rescaled-space. Usually, when using auto-rescaling, a good starting value for $ \rho _{start}$ is $ 0.1$. This will make the algorithm very robust against noise. Depending on the noise level and on the experience you have with your objective function, you may, at a later time, decide to reduce $ \rho _{start}$.

Parallel CONDOR

The different evaluations of $ \mbox{$\cal F$}$$ (x)$ are used to:

(a)
guide the search to the minimum of $ \mbox{$\cal F$}$$ (x)$ (see evaluation performed at step 4: computation of the ``degree of agreement'' $ \tau_k$). To guide the search, the information gathered until now and available in $ \mbox{$\cal Q$}$$ _k(\delta)$ is exploited.
(b)
increase the quality of the approximator $ \mbox{$\cal Q$}$$ _k(\delta)$ (see evaluation performed at step 2). To avoid the degeneration of $ \mbox{$\cal Q$}$$ _k(s)$, the search space needs to be additionally explored.

(a) and (b) are antagonist objectives like it is usually the case in the exploitation/exploration paradigm. The main idea of the parallelization of the algorithm is to perform the exploration on distributed CPU's. Consequently, the algorithm will have better models $ \mbox{$\cal Q$}$$ _k(\delta)$ of $ \mbox{$\cal F$}$$ (x)$ at its disposal and choose better search directions, leading to a faster convergence.

When the dimension of the search space is low, there is no need to make many samples of $ \mbox{$\cal F$}$$ (x)$ to obtain a good approximation $ \mbox{$\cal Q$}$$ _k(\delta)$. Thus, the parallel algorithm is more useful for large dimension of the search space.

XML-Based interface to CONDOR

The CONDOR optimizer is taking as parameter on the command-line the name of a XML file containing all the required information needed to start the optimization process.


File structure of the XML-based configuration file

Let's start with a simple example: 

<?xml version="1.0" encoding="ISO-8859-1"?>
<configCONDOR>
    <!--  name of all design variables (tab separated) -->
    <varNames dimension="4">
        x1 x2 x3 x4
    </varNames>

    <objectiveFunction nIndex="5">

         <!--- name of the outputs which are computed by the
          simulator. If not enough names are given, the same
          names are used many times with a different prefixed
          number (tab separated) -->
        <indexNames>
             indexA indexB
        </indexNames>

        <!-- the aggregation function -->
        <aggregationFunction>

              indexA_1+indexB_1+indexA_2+indexB_2+indexA_3

              <!-- if there are several sub-objective,
              specify them here:
              <subAggregationFunction name="a">
              </subAggregationFunction> -->

        </aggregationFunction>

        <!-- blackbox objective function -->
        <executableFile>
             OF/testOF
        </executableFile>

        <!-- objective function: input file -->
        <inputObjectiveFile>
            optim.out
        </inputObjectiveFile>

        <!-- objective function: output file -->
        <outputObjectiveFile>
            simulator.out
        </outputObjectiveFile>

        <!-- optimization of only a part of the variables -->
        <variablesToOptimize>
            <!-- 1  2  3  4   -->
                 1  1  1  1
        </variablesToOptimize>
    </objectiveFunction>

    <!-- a priori estimated x (starting point) -->
    <startingPoint>
    <!--    1      2    3    4  -->
         -1.2   -1.0   -1    3
    </startingPoint>

    <constraints>
        <!-- lower bounds for x -->
        <lowerBounds>
            <!--
              1   2   3   4 -->
            -10 -10 -10 -10
        </lowerBounds>

        <!-- upper bounds for x -->
        <upperBounds>
            <!--
             1  2  3  4 -->
            10 10 10 10
        </upperBounds>

        <!-- Here would be the matrix for linear
             inequalities definition if they were needed
        <linearInequalities>
            <eq>
            </eq>
        </linearInequalities> -->

        <!-- non-Linear Inequalities
        <nonLinearInequalities>
            <eq>
            </eq>
        </nonLinearInequalities> -->

        <!-- non-Linear equalities
        <equalities>
            <eq>
            </eq>
        </equalities> -->
    </constraints>

    <!-- scaling factor for the normalization of
         the variables (optional) -->
    <scalingFactor auto />

    <!-- parameter for optimization:
          *rho_start: initial distance between
               sample sites (in the rescaled space)
          *rho_end: stopping criteria(in the
               rescaled space)
          *timeToSleep: when waiting for the result
               of the evaluation of the objective
               function, we check every xxx seconds
               for an appearance of the file containing
               the results (in second).
          *maxIteration: maximum number of iteration
    -->
    <optimizationParameters
        rhostart    =".1  "
        rhoend      ="1e-3"
        timeToSleep =".1  "
        maxIteration="1000"
    />

    <!-- all the datafile are optional:
       *binaryDatabaseFile: the filename of the full
            DB data (WARNING!! BINARY FORMAT!)
       *asciiDatabaseFile: data to add to the full DB
            data file (in ascii format)
       *traceFile: the data of the last run are inside
            a file called? (WARNING!! BINARY FORMAT!) -->
    <dataFiles
        binaryDatabaseFile="dbEvalsQ4N.bin"
        asciiDatabaseFile="dbEvalsQ4N.txt"
        traceFile="traceQ4N.bin"
    />

    <!-- name of the save file containing the end
         result of the optimization process -->
    <resultFile>
        traceQ4N.txt
    </resultFile>

    <!-- the sigma vector is used to compute sensibilities
         of the Obj.Funct. relative to variation of
         amplitude sigma_i on axis i -->
    <sigmaVector>
        1 1 1 1
    </sigmaVector>

</configCONDOR>

All the extra tags which are not used by CONDOR are simply ignored. You can thus include additional information inside the configuration file without any problem (it's usually better to have one single file which contains everything which is needed to start an optimization run). The full path to the XML file is given as first command-line parameter to the executable which evaluates the objective function.

The varNames tag describes the name of the variables we want to optimize. These variables will be referenced thereafter as design variables. These are three equivalent definitions of the same design variable names: 

    <varNames dimension="2" />

    <varNames> X_01 X_02 </varNames>

    <varNames dimension="2"> X_01 X_02 </varNames>
In the last case, the dimension attribute and the number of name given inside the varNames tag must match. When giving specific name, each name is separated from the next one by either a space, a tabulation or a carriage return (unix,windows). The varNames tag also describes what's the dimension of the search space. Let's define $ n$, the dimension of the search space.

The objectiveFunction tag describes the objective function. Usually, each evaluation of the objective function is performed by an external executable. The name of this executable is specified in the tag executableFile. This executable takes as input a file which contains the point where the objective function must be evaluated. The name of this file is specified in the tag inputObjectiveFile. In return, the executable write the result of the evaluation inside a file specified in the tag outputObjectiveFile. When CONDOR runs the executable, it gives three extra parameters on the command-line: the full path to the XML-configuration file, the inputObjectiveFile and the outputObjectiveFile. The result file outputObjectiveFile contains a vector $ V_{iv}$ of numbers called index variables.

There are 2 ways to specify the dimension of $ V_{iv}$:

  1. Use the nIndex attribute
  2. If the nIndex attribute is missing then the dimension of $ v_{iv}$ is the number of index variable names given inside the tag indexNames

Let's define $ nIndex$, the number of index variables. We have: $ \displaystyle V_{iv} \in \Re^{nIndex}$. The values inside $ V_{iv}$ will be saved inside an internal database. They will be used to enable ``hot start''. Each index variable has a name. The following example demonstrates two equivalent definition of the same three index variable names: 
    <objectiveFunction nIndex="3">
        ...

    <objectiveFunction>
        <indexNames> Y_001 Y_002 Y_003 </indexNames>
        ...
These are two equivalent definition of the same six index variable names: 
    <objectiveFunction nIndex="6">
        <indexNames> U V </indexNames>
        ...

    <objectiveFunction>
        <indexNames> U_1 V_1 U_2 V_2 U_3 V_3 </indexNames>
        ...

Suppose you want to optimize a seal design. For a seal optimization, we want to minimize the leakage at low speed and high pressure(1), minimize the efficiency-loss due to friction at high speed(2), maximize the ``lift'' at low speed and low pressure(3). The overall quality of a specific design of a seal, we will be computed based on 3 different simulations of the same seal design at the following three operating point: low speed and high pressure(1), high speed(2), low speed and low pressure(3). Suppose each run of the simulator gives as result four index variables: A,B,C,D. We will have the following XML configuration (the content of the aggregationFunction tag will be explained hereafter): 

    ...
    <objectiveFunction nIndex="12">
        <indexNames> A B C D </indexNames>
        <aggregationFunction>
              <subAggregationFunction name="leakage">
                  <!-- compute the leakage based on A_1, B_1, C_1, D_1 -->
                  5*(A_1^3)
              </subAggregationFunction>
              <subAggregationFunction name="friction_loss">
                  <!-- compute the efficiency loss due to friction
                       based on A_2, B_2, C_2, D_2 -->
                  2.1*(-B_1^2+C_1^2)
              </subAggregationFunction>
              <subAggregationFunction name="lift">
                  <!-- compute the ``lift'' based on A_3, B_3, C_3, D_3 -->
                  0.5*(sqrt(D_3))
              </subAggregationFunction>
        </aggregationFunction>
        ...

All the values of the index variables) must be aggregated into one number which will be optimized by CONDOR. The aggregation function is given in the tag
aggregationFunction. If this tag is missing, CONDOR will use as aggregation function the sum of all the index variables.

You can define inside the tag aggregationFunction, some sub-objectives. Each sub-objective is defined inside the tag subAggregationFunction. The tag subAggregationFunction can have an optional parameter name which will appear inside the tracefile. The global aggregation function is the sum of all the sub-objectives. You can look inside the trace-file of the optimization process to see how the different subobjectives are comparing together and adjust accordingly the equations defining the subobjectives. Typically, this procedure is iterative: you define some approximate sub-objectives functions, you run CONDOR, you observe ``where'' CONDOR is heading for, you look inside the trace file to see what's the reason of such direction, you adjust the different sub-objectives giving more or less weight to specific sub-objectives and you restart CONDOR, etc.

The aggregationFunction tag or the subAggregationFunction tag contains simple equations which can have as ``input variables'' all the design variables and all the index variables. The mathematical operators that are allowed are: $ +,-,*,/,\hat{},exp$, $ log$ (base:$ e$), $ sqrt$, $ sin$, $ cos$, $ tan$, $ ctan$, $ asin$, $ acos$, $ atan$, $ actan$, $ sinh$, $ cosh$, $ tanh$, $ ctanh$, $ asinh$, $ acosh$, $ atanh$, $ actanh$, $ fabs$.

In the example above (about seal design), the sub-objectives are the leakage, the efficiency-loss due to friction and the ``lift''. The weights of the different sub-objectives have been adjusted to respectively 5, 2.1 and 0.5 by the design engineer. The values of the index variables A_1, B_1, C_1, D_1, A_2, B_2, C_2, D_2, A_3, B_3, C_3, D_3 for all the different computed seal designs have been saved inside the database of CONDOR and can be re-used to ``hot-start'' CONDOR. The initialization phase of CONDOR is usually time consuming because we need to compute many samples of the objective function $ \mbox{$\cal F$}$$ (x)$ to build the first $ \mbox{$\cal Q$}$$ _k(\delta)$). The initialization phase can be strongly shortened using the ``hot-start''.

If none of the aggregation functions and none of the sub-aggregation functions are using any index variables, you can omit the indexNames, executableFile, inputObjectiveFile and outputObjectiveFile tags. You can also omit the nIndex attribute of the objectiveFunction tag and the timeToSleep attribute of the optimizationParameters tag. The attributes binaryDatabaseFile and asciiDatabaseFile of the dataFiles tag are ignored. This feature in mainly useful for quick demonstration purposes.

The variablesToOptimize tag defines which design variables CONDOR will optimize. This tag contains a vector $ O$ of dimension $ n$ ( $ O \in \Re^n$). If $ O_i$ equals 0 the design variable of index $ i$ will not be optimized.

The startingPoint tag defines what's the starting point. It contains a vector $ x_{start}$ of dimension $ n$. If this tag is missing, CONDOR will use as starting point the best point found inside its database. If the database is empty, then CONDOR issues an error and stops.

The constraints tag defines what are the constraints. It's an optional tag. It contains the tags lowerBounds and upperBounds which are self explanatory. It also contains the tag linearInequalities which describes linear inequalities. If the feasible space is described by the following three linear inequalities:

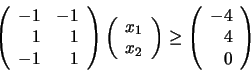
\begin{displaymath}\left( \begin{array}{rr} -1 & -1 \\ 1 & 1 \\ -1 & 1 \end{ar... ...geq \left( \begin{array}{r} -4 \\ 4 \\ 0 \end{array} \right) \end{displaymath}

then we will have: 
    <constraints>
        <linearInequalities>
        -1 -1 -4
         1  1  4
        -1  1  0
        </linearInequalities>
        ...
or by: 
    <constraints>
        <linearInequalities>
             <eq> -1 -1 -4 </eq>
             <eq>  1  1  4 </eq>
             <eq> -1  1  0 </eq>
        </linearInequalities>
        ...
A carriage return or a <eq>..</eq> tag pair is needed to separate each linear inequality. The two notations cannot be mixed. The constraints tag also contains the nonLinearInequalities tag which describes non linear inequalities $ c_i(x)$. The feasible space is described by $ c_i(x)\geq 0 \;\; \forall i$. Each non-linear inequalities $ c_i(x)$ must be defined inside a separate <eq>..</eq> tag pair. For example the two non-linear constraints $ 1-x_0^2-x_1^2 \geq 0$ and $ x_1-x_0^2 \geq 0$ are defined by: 
    ...
    <varNames> x0 x1 </varNames>
    ...
    <constraints>
        <nonLinearInequalities>
            <eq> 1-x0*x0-x1*x1 </eq>
            <eq> -x0*x0+x1      </eq>
        </nonLinearInequalities>
        ...
If there is only one non-linear inequality, you can write it directly, without the eq tags. CONDOR also handles a primitive form of equality constraints. The equalities must be given in an explicit way. For example: 
    ...
    <varNames> x0 x1 x2 </varNames>
    <constraints>
        <equalities> x2=(1-x0)^2 </equalities>
        ...
(the <eq>...</eq> tag pair has been omitted because there is only one equality).

The re-scaling factors $ r_i, \;\; i=1,\ldots,n$ are defined inside the scalingFactor tag. For more information about the re-scaling factors, see section 1.3.4. If the re-scaling factors are missing, CONDOR assumes $ r_i=1 \;\; \forall i$. To have automatic computation of the re-scaling factors, write: 

    <scalingFactor auto/>
The optimizationParameters tag contains the following attributes:

The dataFiles tag contains the following attributes:

All binary files can be converted to ASCII files using the 'matConvert.exe' utility.

The name of the file containing the end result of the optimization process is given inside the resultFile tag. This is an ascii file which contains: the dimension of search-space, the total number of function evaluation (total NFE), the number of function evaluation before finding the best point, the value of the objective function at solution, the solution vector $ x^*$, the Hessian matrix at the solution $ H^*$, the gradient vector at the solution $ g^*$ (it should be zero if there is no active constraint), the lagrangian Vector at the solution (for lower,upper,linear,non-linear constraints), the sensitivity vector.

The sigma vector which is used to compute sensibilities of the Objective Function relatively to variation of amplitude $ sigma_i$ on axis $ i$ is given inside the sigmaVector tag.

File structure of the inputObjectiveFile

This file contains the point $ x \in \Re^n$ where the objective function must be evaluated. It's an ascii file containing only one line. This line contains all the component $ x_i$ of $ x$ separated by a tabulation. The inputObjectiveFile is given as second command-line parameter to the executable which evaluates the objective function.

File structure of the outputObjectiveFile

This file can be ascii or binary. If the first byte of the file is 'A' then the file will be ascii. If the first byte of the file is 'B' then the file will be binary. The outputObjectiveFile is given as third command-line parameter to the executable which evaluates the objective function.

ascii structure

The file contains at least 3 lines:

binary structure

The structure is the following:

File structure of the binaryDatabaseFile

The binaryDatabaseFile is a simple matrix stored in binary format. Each line corresponds to an evaluation of the objective function. You will find on a line all the design variables followed by all the index variables ($ n+nIndex$ numbers).

The utility 'matConvert.exe' converts a full precision binary matrix file to an easy manipulating matrix ascii files.

The structure of the binary matrix file is the following:

File structure of the asciiDatabaseFile

The asciiDatabaseFile is a simple matrix stored in ascii format. Each line of the matrix corresponds to an evaluation of the objective function. You will find on a line all the design variables followed by all the index variables. ($ n+nIndex$ numbers)

The utility 'matConvert.exe' converts a full precision binary matrix file to an easy manipulating matrix ascii files.

The structure of the ascii matrix file is the following:

File structure of the traceFile

The traceFile is a simple matrix stored in binary format. The utility 'matConvert.exe' converts a full precision binary matrix file to an easy manipulating matrix ascii files. Each line of the matrix corresponds to an evaluation of the objective function. You will find on a line:

  1. All the design variables ($ n$ numbers)
  2. All the sensibilities computed using the Sigma vector. ($ n$ numbers)
  3. The global sensibility (the sum of all the sensibilities). ($ 1$ number)
  4. If some subAggregationFunction are defined, you will find their value here ($ ?$ numbers)
  5. The value of the objective function which is the result of the aggregation process ($ 1$ number)
  6. A flag which indicates if the evaluation considered on this line has failed. If this flag is 1 then there have been a failure. This flag is normally zero (no failure of the evaluation of the objective function). ($ 1$ number)

Examples

Most of the time, when researchers are confronted to a noisy optimization problem, they are using an algorithm which is a combination of Genetic Algorithm and Neural Network. This algorithm will be referred in the following text under the following abbreviation: (GA+NN). The principle of this algorithm is the following:

  1. Sample the objective function at different points of the space to obtain an initial database of evaluation.
  2. Use the database of evaluation to build a Neural Network approximation of the real objective function $ \mbox{$\cal F$}$$ (x)$ that we want to optimize.
  3. Use a genetic algorithm to find the minimum $ X_k$ of the Neural Network build at the previous step. Evaluate $ \mbox{$\cal F$}$$ (X_k)$ and add the result of the evaluation to the database of evaluation.
  4. if termination criteria is not met go back to step 2.

This approach has no proof of convergence and there is no guarantee that it will find a simple local minimum. In opposition CONDOR is part of a family of optimizers which are always convergent to a local optimum. The (GA+NN) approach can be made globally convergent using a surrogate approach [KLT97,BDF$^+$99]. The surrogate approach has a strong mathematical background and is assured to always converge to a local minimum.

Simple standard case (no failure)

A xml-configuration file for the standard case is given in section 2.1. You can run this example with the script file named 'testQ4N'. The objective function is computed in an external executable and is:

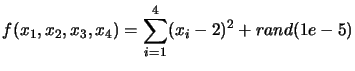
$\displaystyle f(x_1,x_2,x_3,x_4) = \sum_{i=1}^4 (x_i-2)^2 + rand(1e-5) $

where $ rand(t)$ is a random number with uniform distribution which is between 0 and $ t$ ( $ 0 \leq rand(t)<t$). This random number simulates the noise inside the evaluation of the objective function. An interesting test to perform is to change the variablesToOptimize tag and re-run CONDOR. Using the database of old evaluation, CONDOR will build the first quadratical approximation $ \mbox{$\cal Q$}$$ _k(\delta)$ of $ \mbox{$\cal F$}$$ (x)$ (see step 1. of the algorithm) without requiring the normal, classical large number of evaluations. CONDOR will start ``for free''. Figure 2.1 is representing the trace of 100 runs of the optimizer (with a noise of amplitude $ 1e-4$). You can see on figure 2.1 that usually after 50 evaluations of the objective function, we find the optimum. Because of the noise, CONDOR continues to sample the objective function and does not stop immediately.

Figure 2.1: the trace of some runs of the optimizers
\begin{figure}\centering\epsfig{figure=figures/noise2.eps, width=7.5cm, height=5cm}\end{figure}

The script-file named 'testQ4N' optimizes the same objective function but, this time, without noise. Using CONDOR we obtain:

Simple standard case (with failures)

The xml-configuration file for this example is given is section 2.1. The content of the tag executableFile needs to be changed: it must be replace by "OF/testOFF". You can run this example with the script file named 'testQ4NF'. The objective function is the same as in the previous subsection: a simple 4 dimensional quadratic centered at $ (2,2,2,2)$ and perturbated with a noise of maximum amplitude $ 1e-5$. The failure are simulated using a random number:

if rand(1.0)>.55 then fail else succeed.

The evaluation of the objective function at the given starting point cannot fail. If this happens, CONDOR has no starting point and it stops immediately.

The classical Rosenbrock Objective function

The xml-configuration file for this example is the following: 

<?xml version="1.0" encoding="ISO-8859-1"?>
<configCONDOR>
    <varNames> x_1 x_2 </varNames>
    <objectiveFunction>
        <aggregationFunction>
            100*(x_2-x_1^2)^2+(1-x_1)^2
        </aggregationFunction>
    </objectiveFunction>
    <startingPoint> -1.2   -1.0 </startingPoint>
    <constraints>
        <lowerBounds> -10 -10 </lowerBounds>
        <upperBounds>  10 10  </upperBounds>
    </constraints>
    <optimizationParameters
        rhostart    =" 1    "
        rhoend      =" 1e-2 "
        maxIteration=" 1000 "
    />
    <dataFiles traceFile="traceRosen.dat" />
    <resultFile> resultsRosen.txt </resultFile>
    <sigmaVector> 1 1 </sigmaVector>
</configCONDOR>
You can run this example with the script file named 'testRosen'. In the optimization community this function is a classical test-case. The minimum of the function is at 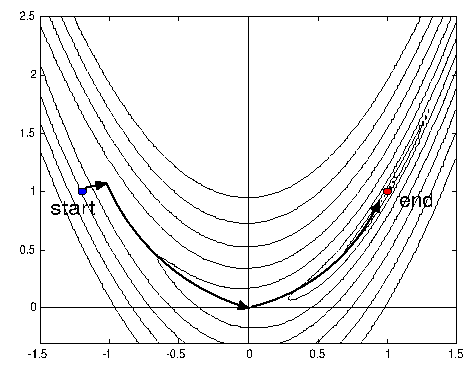$ (1,1)$. To reach it the optimizer must follow the bottom of a narrow ``valley''. The edge of the valley are very steep and the bottom is nearly flat. It's thus very difficult to find the right direction to follow. Following the slope is even more difficult as the search direction in the valley is changing continuously. See figure 2.2 for an illustration of the Rosenbrock function.
Figure 2.2: The Rosenbrock function
\begin{figure}\centering\epsfig{figure=figures/rosen.eps, width=12cm, height=9cm}\end{figure}

For optimizers which are following the slope (like CONDOR), this function is a real challenge. In opposition, (GA+NN) optimizers are not using the concept of slope and should not have any special difficulties to find the minimum of this function. Beside (GA+NN) are most efficient on small dimensional search space (in opposition to CONDOR). They should thus exhibit very good performances compared to CONDOR on this problem. Using CONDOR we obtain:

The performances of CONDOR on this problem (compared to the performances of (GA+NN) optimizers) are rather low, as expected (a typical (GA+NN) optimizer requires at least 140 evaluations of the objective function (usually:800 evaluations) for less precision on the minimum). In this example, CONDOR cannot go ``directly'' to the minimum: it must avoid the big ``bump'' in the function and pass through the point $ (0,0)$ before being allowed to ``fall'' into the minimum. This explains why the performances of CONDOR are poor. In opposition, a (GA+NN) algorithm starts by sampling all the space. This strategy allows to start from a point which is already on the right side of the barrier (a point which has $ x_1>0$). Starting from there, there is no ``bump'' anymore to avoid.

A future extension of CONDOR will be able to start simultaneously from different points of the space. It will then exchange information between each trajectory to increase convergence speed. This new strategy should increase the convergence speed substantially on such problems.

A simple quadratic in two dimension

In the previous subsection, we have seen that the performances of CONDOR on the Rosenbrock function are low because the optimizer must avoid a ``barrier'' inside the objective function before it can ``home'' to the minimum. What happens if we remove this barrier? Let's consider the following xml-configuration file: 

<?xml version="1.0" encoding="ISO-8859-1"?>
<configCONDOR>
    <varNames> x_0 x_1 </varNames>
    <objectiveFunction>
        <aggregationFunction>  (x_1-2)^2+(x_0-2)^2   </aggregationFunction>
    </objectiveFunction>
    <startingPoint> 0   0 </startingPoint>
    <constraints>
        <lowerBounds> -10 -10 </lowerBounds>
        <upperBounds>  10  10 </upperBounds>
    </constraints>
    <scalingFactor auto/>
    <optimizationParameters
        rhostart    =" 1    "
        rhoend      =" 9e-1 "
        maxIteration=" 1000 "
    />
    <dataFiles traceFile="traceQ2.dat" />
    <resultFile> resultsQ2.txt </resultFile>
    <sigmaVector> 1 1 </sigmaVector>
</configCONDOR>
You can run this example with the script file named 'testQ2'. Using CONDOR we obtain: As comparison, a (GA+NN) algorithm requires between 150 and 500 evaluations of the objective function before reaching an approximative optimum point (the value of the objective function is around 1e-12). Beside, the performances of (GA+NN) optimizers are dropping very rapidly when the search space dimension increases.

A badly scaled objective function

The xml-configuration file for this example is the following: 

<?xml version="1.0" encoding="ISO-8859-1"?>
<configCONDOR>
    <varNames> x0 x1 </varNames>
    <objectiveFunction>
        <aggregationFunction>
            100*(x1/1000-x0^2)^2+(1-x0)^2
        </aggregationFunction>
    </objectiveFunction>
    <startingPoint> -1.2   -1000 </startingPoint>
    <constraints>
        <lowerBounds> -10 -10000 </lowerBounds>
        <upperBounds>  10  10000  </upperBounds>
    </constraints>
    <scalingFactor auto/>
    <optimizationParameters
        rhostart    =" .1    "
        rhoend      =" 1e-5 "
        maxIteration=" 1000 "
    />
    <dataFiles traceFile="traceScaledRosen.dat"  />
    <resultFile> resultsScaledRosen.txt </resultFile>
    <sigmaVector> 1 1 </sigmaVector>
</configCONDOR>

You can run this example with the script file named 'testScaledRosen'. As explained in section 1.3.4, the design variables x0 and x1 must be in the same order of magnitude to obtain high convergence speed. This is not the case here: x1 is 1000 times greater than x0. Some appropriate re-scaling factors are computed by CONDOR and applied. Using CONDOR we obtain:

After removing the line <scalingFactor auto/>, we obtain: This demonstrates the importance of the scaling factors.

Optimization with linear and box constraints

One technique to deal with linear and box constraints is the ``Gradient Projection Methods''. In this method, we follow the gradient of the objective function. When we enter the infeasible space, we will simply project the gradient into the feasible space. The convergence speed of this algorithm is, at most, linear, requiring many evaluation of the objective function.

A straightforward (unfortunately false) extension to this technique is the ``Newton Step Projection Method''. This technique should allow (if it works) a very high (quadratical) speed of convergence. It is illustrated in figure 2.3. This method is the following:

  1. Construct a quadratic approximation $ \mbox{$\cal Q$}$$ _k(\delta)$ of $ \mbox{$\cal F$}$$ (x)$ around the current point $ x_k$.
  2. Find the minimum $ \delta_k$ of $ \mbox{$\cal Q$}$$ _k(\delta)$ and go to $ x_k+\delta_k$. $ \delta_k$ is called the ``Newton Step''.
  3. If $ x_k+\delta_k$ is feasible then $ x_{k+1}=x_k+\delta_k$.
    If $ x_k+\delta_k$ is infeasible then project it to the feasible space. This projection is $ x_{k+1}$.
  4. If stopping criteria not met, go back to step 1.

In figure 2.3, the current point is $ x_k=O$. The Newton step ($ \delta_k$) lead us to point P which is infeasible. We project P into the feasible space: we obtain B. Finally, we will thus follow the trajectory OAB, which seems good.

Figure 2.3: "newton's step projection algorithm" seems good.
\begin{figure}\centering\epsfig{figure=figures/gradprojeter.eps, width=5.2cm, height=5.5cm}\end{figure}

In figure 2.4, we can see that the "Newton step projection algorithm" can lead to a false minimum. As before, we will follow the trajectory OAB. Unfortunately, the real minimum of the problem is C.

Figure 2.4: "Newton's step projection algorithm" is failing.
\begin{figure}\centering\epsfig{figure=figures/gradprojeter2.eps, width=6cm, height=5cm}\end{figure}

Despite its wrong foundation, the ``Newton Step Projection Method'' is very often encountered [BK97,Kel99,SBT$^+$92,GK95,CGP$^+$01]. CONDOR uses an other technique based on active-set method which allows very high (quadratical) speed on convergence even when ``sliding'' along a constraint.

Let's have a small example: 

<?xml version="1.0" encoding="ISO-8859-1"?>
<configCONDOR>
    <varNames> x0 x1 </varNames>
    <objectiveFunction>
        <aggregationFunction>   (x0-2)^2+(x1-5)^2    </aggregationFunction>
    </objectiveFunction>
    <startingPoint> 0  0 </startingPoint>
    <constraints>
        <lowerBounds>   -2 -3  </lowerBounds>
        <upperBounds>    3  3  </upperBounds>
        <linearInequalities>
            <eq>   -1   -1   -4 </eq>
        </linearInequalities>
    </constraints>
    <scalingFactor auto/>
    <optimizationParameters
        rhostart    =" 1    "
        rhoend      =" 1e-2 "
        maxIteration=" 1000 "
    />
    <dataFiles traceFile="traceSuperSimple.dat"    />
    <resultFile>    resultsSuperSimple.txt     </resultFile>
    <sigmaVector>  1 1  </sigmaVector>
</configCONDOR>

Figure 2.5: Optimization with Linear and Box constraints
\begin{figure}\centering\epsfig{figure=figures/ssimple.eps, width=9.5cm, height=9cm}\end{figure}

You can run this example with the script file named 'testSuperSimple'. This problem is illustrated in figure 2.5. Using CONDOR, we obtain

At the solution, the upper bound on variable $ x1$ and the first linear constraint are active.

Optimization with non-linear constraints

Figure 2.6: Feasible space of Fletcher's problem
\begin{figure}\centering\epsfig{figure=figures/fletcher2.eps, width=9cm, height=6cm}\end{figure}

The xml-configuration file for this example is the following: 

<?xml version="1.0" encoding="ISO-8859-1"?>
<configCONDOR>
    <varNames> v0 v1 </varNames>
    <objectiveFunction>
        <aggregationFunction>    -v0   </aggregationFunction>
    </objectiveFunction>
    <startingPoint>  0   0  </startingPoint>
    <constraints>
        <!-- non-Linear Inequalities: v is feasible <=> c_i(v)>=0 -->
        <nonLinearInequalities>
            <eq> 1-v0*v0-v1*v1 </eq>
            <eq> v1-v0*v0      </eq>
        </nonLinearInequalities>
    </constraints>
    <optimizationParameters
        rhostart    =" .1   "
        rhoend      =" 1e-6 "
        maxIteration=" 1000 "
    />
    <dataFiles traceFile="traceFletcher.dat"  />
    <resultFile> resultsFletcher.txt  </resultFile>
    <sigmaVector> 1 1 </sigmaVector>
</configCONDOR>

You can run this example with the script file named 'testFletcher'. The feasible space is illustrated in figure 2.6. Using CONDOR, we obtain

C++ code interface.

In preparation.

Some useful remarks and tricks.

Typical behavior of CONDOR

Figure 4.1: Optimization trace
\begin{figure}\centering\epsfig{figure=figures/trace.eps, width=10cm, height=7.5cm}\end{figure}

You can see in figure 4.1 a trace of an optimization run of CONDOR. On the x-axis, you have the time $ t$. On the y-axis you have the value of the objective function which has been computed at time $ t$.

CONDOR always starts by sampling the objective function to build the initial quadratical approximation $ \mbox{$\cal Q$}$$ _0(\delta)$ of $ \mbox{$\cal F$}$$ (x)$ around $ x_{start}$ (see section 1.2 - step 1: Initialization). This is called the sampling/initial construction phase. During this phase the optimizer will not follow the slope towards the optimum. Therefore the values of the objective function remains more or less the same during all the sampling phase (as you can see in figure 4.1). Once this phase is finished, CONDOR has enough information to be able to follow the slope towards the minimum. The information gathered up to now during the sampling phase are finally used. This is why, usually, just after the end of the sampling phase, there is a significant drop inside the value of the objective function (see figure 2.1).

This first construction phase requires $ \frac{1}{2}(n+1)(n+2) $ evaluations of the objective function ($ n$ is the dimension of the search space). This phase is thus very lengthy. Furthermore, during this phase, the objective function is usually not ``reduced''. The computation time can be strongly reduced if you use ``hot start''. Another possibility to reduce the computation time is to use the parallel version of CONDOR. This phase can be parallelized very easily and without efficiency-loss. If you use $ N=\frac{1}{2}(n+1)^2$ computers in parallel the computation time of the sampling phase will be reduced by $ N$.

From time to time CONDOR is making a ``perpendicular'' or ``model improvement'' step. The aim of this step is to avoid the degeneration of the quadratical approximation $ \mbox{$\cal Q$}$$ _k(\delta)$ of $ \mbox{$\cal F$}$$ (x)$. Thus, when performing a ``model improvement'' step, CONDOR will not try to follow the slope of the objective function and will produce (most of the time) a very bad values of $ \mbox{$\cal F$}$$ (x)$.

Shape optimization: parametrization trick.

Let's assume you want to optimize a shape. A shape can be parameterized using different tools:

Let's assume we have parameterized the shape of a blade using ``Bezier curves''. An illustration of the parametrization of an airfoil blade using Bezier curves is given in figures 4.2 and 4.3.

Figure 4.2: Superposition of thickness normal to camber to generate an airfoil shape
\begin{figure}\centering\epsfig{figure=figures/bezier.eps, width=12cm, height=4.5cm}\end{figure}

Figure 4.3: Bezier control variable required to form an airfoil shape
\begin{figure}\centering\epsfig{figure=figures/bezier2.eps, width=12cm, height=7.5cm}\end{figure}

Some set of shape parameters generates infeasible geometries. The ``feasible space'' of the constrained optimization problem is defined by the set of parameters which generates feasible geometries. A good parametrization of the shape to optimize should only involve box or linear constraints. Non-linear constraints should be avoided.

In the airfoil example, if we want to express that the thickness of the airfoil must be non-null, we can simply write $ b_8>0, b_{10}>0, b_{14}>0$ (3 box constraints) (see Figure 4.3 about $ b_8, b_{10}$ and $ b_{14}$). Expressing the same constraint (non-null thickness) in an other, simpler, parametrization of the airfoil shape (direct description of the upper and lower part of the airfoil using 2 bezier curves) can lead to non-linear constraints. The parametrization of the airfoil proposed here is thus very good and can easily be optimized.

A note about the variablesToOptimize tag

Figure 4.4: Illustration of the slow linear convergence when performing consecutive optimization runs with some variables deactivated.
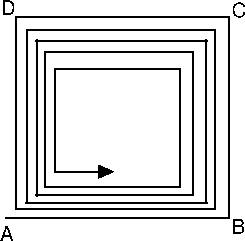\begin{figure}\centering\epsfig{figure=figures/slowConvergence.eps, width=5.5cm, height=5.5cm}\end{figure}

If you want, for example, to optimize $ n+m$ variables, never do the following:

This algorithm will results in a very slow linear speed of convergence as illustrated in Figure 4.4. The config-file-parameter variablesToOptimize allows you to activate/deactivate some variables, it's sometime a useful tool but don't abuse from it! Use with care!

Sensibilities

Sigma vector ( $ \sigma \in \Re ^n$)

Let's apply a small perturbation $ sigma_i$ to the optimum point $ \bar{x}^*$ in the direction $ \bar{e_i}$. Let's assume that the objective function is minimum at $ \bar{x}^*$. How much does this perturbation increase the value of the objective function?

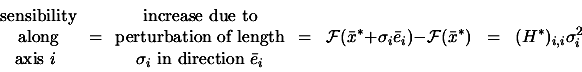\begin{displaymath}\begin{array}{c} \text{sensibility} \\ \text{along} \\ \tex... ...- \mbox{$\cal F$}(\bar{x}^*) \;\; = \;\; (H^*)_{i,i} \sigma_i^2\end{displaymath} (4.1)

The sigma vector is used to check the sensibilities of the objective function relative to small perturbation on the coordinates of $ x^*$. If $ x^*$ represents the optimal design for a shape, the sigma vector help us to see the impact on the objective function of the manufacturing tolerances of the optimal shape.

The same result can be obtained when convoluting the objective function with a gaussian function which has as variances the $ sigma_i$'s.

Lagrangian vector

One of the output CONDOR is giving at the end of the optimization process is the lagrangian Vector $ \lambda^*$ at the solution. What's useful about this lagrangian vector?

We define the classical Lagrangian function $ \L $ as:

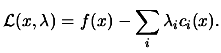$\displaystyle \L (x, \lambda)= f(x)-\sum_i \lambda_i c_i(x).$ (4.2)

where the $ \lambda_i$ are the Lagrangian variables or Lagrangian multipliers associated with the constraints. In constrained optimization, we find an optimum point ( $ x^*, \lambda^*$), called a KKT point (Karush-Kuhn-Tucker point) when:
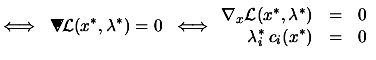$\displaystyle (x^*, \lambda^*)$    is a KKT point $\displaystyle \Longleftrightarrow \;\; \begin{picture}(.27,.3) \put(0,0){\makeb... ...abla_x \L (x^*,\lambda^*) &= & 0 \\ \lambda_i^* \: c_i(x^*) & = & 0 \end{array}$ (4.3)
where $\displaystyle \begin{picture}(.27,.3) \put(0,0){\makebox(0,0)[bl]{$\nabla$}} \p... ...cture} = \left( \begin{array}{c} \nabla_x \\ \nabla_\lambda \end{array} \right)$    

The second equation of 4.3 is called the complementarity condition. It states that both $ \lambda^*$ and $ c_i^*$ cannot be non-zero, or equivalently that inactive constraints have a zero multiplier. An illustration is given in figure 4.5.

Figure 4.5: complementarity condition
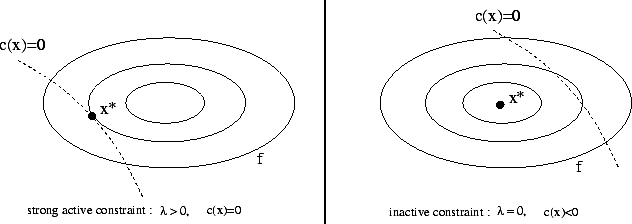\begin{figure}\centering\epsfig{figure=figures/complementarity.eps, width=14cm, height=5cm}\end{figure}

To have some insight into the meaning of Lagrange Multipliers $ \lambda$, consider what happens if the right-hand sides of the constraints are perturbated, so that

$\displaystyle c_i(x)=\epsilon_i, \;\; i \in E\;\;\;\;\;\; (E$    is the set of the active constraints at the solution) (4.4)

Let $ x(\epsilon)$, $ \lambda(\epsilon)$ denote how the solution and lagrangian multipliers are changing as $ \epsilon$ changes. The Lagrangian for this problem is:
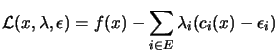$\displaystyle \L (x,\lambda, \epsilon)=f(x)-\sum_{i \in E} \lambda_i (c_i(x)-\epsilon_i)$ (4.5)

From 4.4, $ f(x(\epsilon))=\L (x(\epsilon),\lambda(\epsilon), \epsilon)$, so using the chain rule, we have
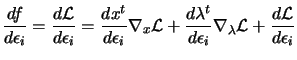$\displaystyle \frac{d f}{d \epsilon_i}=\frac{d \L }{d \epsilon_i}= \frac{d x^t}... ...\frac{d \lambda^t}{d \epsilon_i} \nabla_\lambda \L + \frac{d \L }{d \epsilon_i}$ (4.6)

Using Equation 4.3, we see that the terms $ \nabla_x \L $ and $ \nabla_\lambda \L $ are null in the previous equation. It follows that:
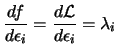$\displaystyle \frac{d f}{d \epsilon_i}= \frac{d \L }{d \epsilon_i} = \lambda_i$ (4.7)

Thus the Lagrange multiplier of any constraint measures the rate of change in the objective function, consequent upon changes in that constraint function. This information can be valuable in that it indicates how sensitive the objective function is to changes in the different constraints.

About virtual constraints and failed evaluations

Figure 4.6: two consecutive failures
\begin{figure}\centering\epsfig{figure=figures/virtualconstraints.eps, width=9cm, height=7.5cm}\end{figure}

Let's consider figure 4.6 which is illustrating two consecutive failure (points A and B) inside the evaluation of the objective function. The part of the search-space where the evaluations are successful is defined by a ``virtual constraint'' (the red line in figure 4.6). We don't have the equation of this ``virtual constraint''. Thus it's not possible to ``slide'' along it. The strategy which is used is simply to ``step back''. Each time an evaluation fails, the trust region radius $ \Delta_k$ is reduced and $ \delta_k$ is re-computed. This indirectly decreases the step size $ \Vert \delta_k \Vert$ since $ \delta_k$ is the solution of:

$\displaystyle \mbox{$\cal Q$}$$\displaystyle (\delta_k) = \min_\delta$   $\displaystyle \mbox{$\cal Q$}$$\displaystyle _k(\delta)$    such that $\displaystyle \frac{\rho_k}{2} < \Vert \delta_k \Vert < \Delta_k$ (4.8)

Inside figure 4.6, the three points A,B,C are aligned. In general, these three points will NOT be aligned since their position is given by equation 4.8 with different values of $ \Delta_k$.

Figure 4.7: Limitations of virtual constraints
\begin{figure}\centering\epsfig{figure=figures/virtualconstraints2.eps, width=9cm, height=7.5cm}\end{figure}

The simple strategy described above has strong limitations. In the example illustrated in figure 4.7, Condor will find as optimal solution the point A. If the same constraint is specified using a box or a linear constraint, Condor will be able to "slide" along it and to find the real optimum point, the point B.


About linked evaluations of the objective function and of constraints

In some cases you obtain as a result of an evaluation of the objective function not only the value of the objective function itself but also the value of a constraint which must be respected. For such constraint (which is linked to the evaluation of the objective function), the strategy to use is the following: use a penalty function.

What's a penalty function? Suppose you want to find:

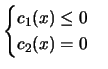
$\displaystyle \min_x f(x)$    subject to $\displaystyle \begin{cases}c_1(x) \leq 0 \ c_2(x)=0 \end{cases} $

The associated penalty function is:

$\displaystyle \min_x f(x)+ \mu_1 \max(c_1(x),0) + \mu_2 c_2(x)$ (4.9)

or you can also use:

$\displaystyle \min_x f(x)+ \mu_1 (\max(c_1(x),0))^2 + \mu_2 (c_2(x))^2$ (4.10)

with $ \mu_1$ and $ \mu_2$ some constants chosen big enough to ``push back'' the optimizer in the feasible space.

Let's assume that you have a small violation of the constraints. In this case, the equation 4.9 will directly penalizes strongly the objective function. Equation 4.9 should be used if you don't want any violation at all at the end, optimal point found by Condor. This is an advantage if equation 4.9. A disadvantage appears when you choose too high values for $ \mu_1$ and $ \mu_2$. This will produce strong non-linearities in the derivatives of the new objective function 4.9 in the part of the search space which is along the constraint (this is known as the Maratos Effect). This will lead to a longer running time for the optimizer. For some extreme values of $ \mu_1$ and $ \mu_2$ the optimizer can fail to find the optimum point of the objective function.

In opposition, the equation 4.10 does not produce any non-linearity in the derivative, even for high values of $ \mu_1$ and $ \mu_2$. This will lead to a short running time for the optimizer. However, small violations of the constraints could be obtained at the end of the optimization process.

When using penalty functions, Condor can enter during the optimization process in the infeasible space. However, if appropriate values are given to $ \mu_1$ and $ \mu_2$, the optimal point found by Condor will be feasible (or, at least, nearly feasible, when using equation 4.10 ).

You can easily define any penalty function inside Condor. All you have to do is to define a subAggregationFunction for each constraints. For example: 

        <aggregationFunction>
              <subAggregationFunction name="main_function">
                 ... computation of f(x) ...
              </subAggregationFunction>
              <subAggregationFunction name="constraint_1">
               100 *  ... computation of c_1(x) ...
              </subAggregationFunction>
              <subAggregationFunction name="constraint_2">
               50 *  ... computation of c_2(x) ...
              </subAggregationFunction>
        </aggregationFunction>
In this example, $ \mu_1= 100$ and $ \mu_2=50$. If you use this facility, Condor will be able to hot-start at every change of $ \mu_1$ and $ \mu_2$. This will lead to a very short optimization time. You will thus be able to precisely adjust $ \mu_1$ and $ \mu_2$.

The extension to multiple linked-constraints is straight forward.

When possible, penalty functions should be avoid. In particular, if you have simple box, linear or non-linear constraints, you should encode them inside the XML file as standard constraints. Condor is using advanced techniques that are (a lot) faster and are more robust in these cases.

Let's assume that you have an objective function that is computing some efficiency measure ( $ 0 < Efficiency \leq 1$ that you want to maximize. You will have something like: 

    <varNames dimension="2">
        x1 x2
    </varNames>
    <objectiveFunction nIndex="1">
        <indexNames> Efficiency </indexNames>
        <aggregationFunction>
              <subAggregationFunction name="good_main_function">
                -1.0 * Efficiency
              </subAggregationFunction>
              ... linked-constrained if any ...
        </aggregationFunction>
        <executableFile>
              ComputeEfficiency.exe
        </executableFile>
        ...
    </objectiveFunction>
You will never define: 
        ...
        <aggregationFunction>
              <subAggregationFunction name="bad_main_function">
                (Efficiency-1)^2
              </subAggregationFunction>
              ...
Let's assume that the objective function $ Efficiency(x_1,x_2)$ has a shape which is close to a quadratic. If you use the good_main_function, CONDOR will ``see'' an objective function that can easily be approximated by a quadratic. CONDOR is using a quadratical approximation $ Q_k(\delta) $ of the objective function to compute the search directions. CONDOR will thus generate good search direction and it will converge very rapidly to the solution of the optimization problem. If you use the bad_main_function, CONDOR will ``see'' an objective function that is of degree 4. It will be difficult to approximate this function with a quadratic. The search direction will thus be of poor quality. The convergence to the optimum will be a lot slower.

A general rule of thumb is: If your objective function ``looks like'' a quadratic, CONDOR will be faster.

In future extension of the optimizer, the variables $ \mu_1$ and $ \mu_2$ will be adjusted automatically.

About constraints violations

Some optimizers which are working with constraints sometimes require to evaluate the objective function in the infeasible space. This is for example the case for the dual-simplex algorithm encountered in linear programming where all the evaluations are in the infeasible space and only the last point of the optimization process (the optimum point) is feasible.

Figure 4.8: Feasibility of the evaluations
\begin{figure}\centering\epsfig{figure=figures/feasible2.eps, width=13cm, height=10.5cm}\end{figure}

Condor is a 99% feasible optimizer. It means that 99% of the evaluations are feasible. Basically, the Condor algorithm moves a cloud of points in the search space towards the optimum point. The center of this cloud is $ x_k$ and is always feasible. See illustration in figure 4.8. The other points (the sampling point) are used to build (using Lagrange interpolation technique) $ \mbox{$\cal Q$}$$ _k(x)$, the local approximation of the objective function $ f(x)$ around $ x_k$. These last points can be in the infeasible space. They are separated from the center point $ x_k$ (which is feasible) by a distance which is at most $ \rho_k$ (see section 1.2 for a complete explanation of these variables). Thus, the length of the violation is at most $ \rho_k$.

You can see in figure 4.8 an illustration of these concepts. The green point is $ x_k$, the center of the cloud, the best point found so far. The blue and red points are sampling points used to build $ \mbox{$\cal Q$}$$ _k(x)$. Some of these sampling points (the red ones) are in the infeasible space. The length of the violation is at most $ \rho_k$.

The external code which computes the objective function should always try to give a correct evaluation of the objective function, even when an evaluation is performed in the infeasible space. It should report a failure (see section 4.5 about failure in computation of the objective function) in the least number of cases.

when using a penalty function (see section 4.6), Condor can enter deeply into the infeasible space. However, at the end of the optimization process, Condor will report the optimal feasible point (only for appropriate values of $ \mu_1$ and $ \mu_2$: see section 4.6 to know more about these variables).

business-insight

Bibliography

BDF$^+$99
Andrew J. Booker, J.E. Dennis Jr., Paul D. Frank, David B. Serafini, Virginia Torczon, and Michael W. Trosset.
A rigorous framework for optimization of expensive functions by surrogates.
Structural Optimization, 17, No. 1:1-13, February 1999.

BK97
D. M. Bortz and C. T. Kelley.
The Simplex Gradient and Noisy Optimization Problems.
Technical Report CRSC-TR97-27, North Carolina State University, Department of Mathematics, Center for Research in Scientific Computation Box 8205, Raleigh, N. C. 27695-8205, September 1997.

BT96
Paul T. Boggs and Jon W. Tolle.
Sequential Quadratic Programming.
Acta Numerica, pages 1-000, 1996.

CAVDB01
R. Cosentino, Z. Alsalihi, and R. Van Den Braembussche.
Expert System for Radial Impeller Optimisation.
In Fourth European Conference on Turbomachinery, ATI-CST-039/01, Florence,Italy, 2001.

CGP$^+$01
R. G. Carter, J. M. Gablonsky, A. Patrick, C. T. Kelley, and O. J. Eslinger.
Algorithms for Noisy Problems in Gas Transmission Pipeline Optimization.
Optimization and Engineering, 2:139-157, 2001.

CGT00
Andrew R. Conn, Nicholas I.M. Gould, and Philippe L. Toint.
Trust-region Methods.
SIAM Society for Industrial & Applied Mathematics, Englewood Cliffs, New Jersey, mps-siam series on optimization edition, 2000.

CGT99
Andrew R. Conn, Nicholas I.M. Gould, and Philippe L. Toint.
Sqp methods for large-scale nonlinear programming.
Technical report, Department of Mathematics, University of Namur, Belgium, 99.
Report No. 1999/05.

DS96
J.E. Dennis Jr. and Robert B. Schnabel.
Numerical Methods for unconstrained Optimization and nonlinear Equations.
SIAM Society for Industrial & Applied Mathematics, Englewood Cliffs, New Jersey, classics in applied mathematics, 16 edition, 1996.

Fle87
R. Fletcher.
Practical Methods of optimization.
a Wiley-Interscience publication, Great Britain, 1987.

GK95
P. Gilmore and C. T. Kelley.
An implicit filtering algorithm for optimization of functions with many local minima.
SIAM Journal of Optimization, 5:269-285, 1995.

Kel99
C. T. Kelley.
Iterative Methods for Optimization, volume 18 of Frontiers in Applied Mathematics.
SIAM, Philadelphia, 1999.

KLT97
Tamara G. Kolda, Rober Michael Lewis, and Virginia Torczon.
Optimization by Direct Search: New Perspectives on Some Classical and Model Methods.
Siam Review, 45 , N°3:385-482, 1997.

Noc92
Jorge Nocedal.
Theory of Algorithm for Unconstrained Optimization.
Acta Numerica, pages 199-242, 1992.

PMM$^+$03
S. Pazzi, F. Martelli, V. Michelassi, Frank Vanden Berghen, and Hugues Bersini.
Intelligent Performance CFD Optimisation of a Centrifugal Impeller.
In Fifth European Conference on Turbomachinery, Prague, CZ, March 2003.

Pol00
C. Poloni.
Multi Objective Optimisation Examples: Design of a Laminar Airfoil and of a Composite Rectangular Wing.
Genetic Algorithms for Optimisation in Aeronautics and Turbomachinery, 2000.
von Karman Institute for Fluid Dynamics.

Pow00
M.J.D. Powell.
UOBYQA: Unconstrained Optimization By Quadratic Approximation.
Technical report, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, England, 2000.
Report No. DAMTP2000/14.

PPGC04
S. Pierret, P. Ploumhans, X. Gallez, and S. Caro.
Turbofan Noise Reduction Using Optimisation Method Coupled To Aero-Acoustic Simulations.
In Design Optimization International Conference, Athens, Greece, March 31-April 2 2004.

PT95
Eliane R. Panier and André L. Tits.
On combining feasibility, Descent and Superlinear Convergence in Inequality Contrained Optimization.
Mathematical Programming, 59:261-276, 1995.

PVdB98
Stéphane Pierret and René Van den Braembussche.
Turbomachinery blade design using a Navier-Stokes solver and artificial neural network.
Journal of Turbomachinery, ASME 98-GT-4, 1998.
publication in the transactions of the ASME: '' Journal of Turbomachinery ''.

SBT$^+$92
D. E. Stoneking, G. L. Bilbro, R. J. Trew, P. Gilmore, and C. T. Kelley.
Yield optimization Using a gaAs Process Simulator Coupled to a Physical Device Model.
IEEE Transactions on Microwave Theory and Techniques, 40:1353-1363, 1992.

VB04
Frank Vanden Berghen.
Optimization algorithm for Non-Linear, Constrained, Derivative-free optimization of Continuous, High-computing-load, Noisy Objective Functions.
Technical report, IRIDIA, Université Libre de Bruxelles, Belgium, may 2004.
Available at http://http://www.applied-mathematics.net.

Frank Vanden Berghen 2004-08-16