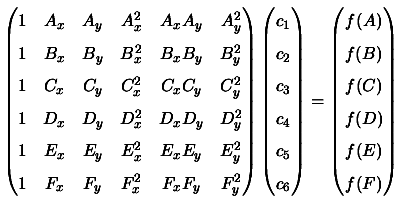


Next: A small reminder about
Up: Multivariate Lagrange Interpolation
Previous: Multivariate Lagrange Interpolation
Contents
One way to generate the local approximation
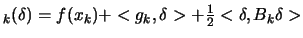 of the objective
function
of the objective
function
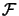
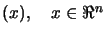 around
around 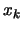 is to make
Multivariate Lagrange Interpolation.
is to make
Multivariate Lagrange Interpolation.
We will sample
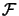 at different points and construct a quadratic
polynomial which interpolates these samples.
at different points and construct a quadratic
polynomial which interpolates these samples.
The position and the number 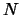 of the points are not random. For
example, if we try to construct a polynomial
of the points are not random. For
example, if we try to construct a polynomial
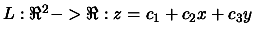 of degree 1 (a plane), which interpolates
locally a function
F
of degree 1 (a plane), which interpolates
locally a function
F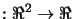 , we need
exactly 3 points
, we need
exactly 3 points  and
and 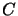 . Why do we need exactly 3
points (apart from the fact that 3 points in 3D determines a
plane)? Because we need to solve for
. Why do we need exactly 3
points (apart from the fact that 3 points in 3D determines a
plane)? Because we need to solve for
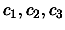 the following
linear system:
the following
linear system:
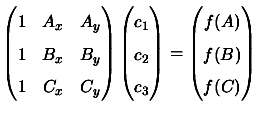 |
(3.1) |
The matrix above is called the ``Vandermonde Matrix''.
We can say even more: What happens if these three points are on
the same line? There is a simple infinity of planes which passes
through three aligned points. The determinant of the Vandermonde
Matrix (called here after the ``Vandermonde determinant'') will be
null. The interpolation problem is not solvable. We will say that
''the problem is NOT poised''.
In opposition to the univariate polynomial interpolation (where we
can take a random number of point, at random different places),
the multivariate polynomial interpolation imposes a precise number
of interpolation points at precise places.
In fact, if we want to interpolate by a polynomial of degree 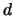 a
function
F
a
function
F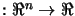 , we will need
, we will need
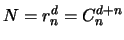 points (with
points (with
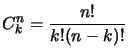 ). If the Vandermonde determinant is not null
for this set of points, the problem is ``well poised''.
). If the Vandermonde determinant is not null
for this set of points, the problem is ``well poised''.
Example: If we want to construct a polynomial
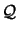
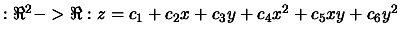 of
degree 2, which interpolates locally a function
F
of
degree 2, which interpolates locally a function
F , at points
, at points
 we will have the
following Vandermonde system:
Beware! Never try to resolve directly Vandermonde systems.
These kind of systems are very often badly conditioned
(determinant near zero) and can't be resolved directly.
we will have the
following Vandermonde system:
Beware! Never try to resolve directly Vandermonde systems.
These kind of systems are very often badly conditioned
(determinant near zero) and can't be resolved directly.
If we already have a polynomial of degree  and want to use
information contained in new points, we will need a block of
exactly
and want to use
information contained in new points, we will need a block of
exactly
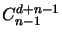 new points. The new interpolating
polynomial will have a degree of
new points. The new interpolating
polynomial will have a degree of  . This is called
''interpolation in block''.
. This is called
''interpolation in block''.



Next: A small reminder about
Up: Multivariate Lagrange Interpolation
Previous: Multivariate Lagrange Interpolation
Contents
Frank Vanden Berghen
2004-04-19
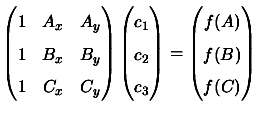
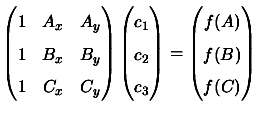
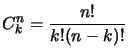 ). If the Vandermonde determinant is not null
for this set of points, the problem is ``well poised''.
). If the Vandermonde determinant is not null
for this set of points, the problem is ``well poised''.