

Next: Lazy Learning, Artificial Neural Networks...
Up: The METHOD project
Previous: Preliminary numerical results
Contents
Subsections
Interface between CONDOR and XFLOS / Pre-Solve phase
We want to optimize optimizes a non-linear function
For the Method project, the objective function
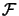
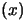 is an
external code (an executable program): XFLOS. I developed a simple
interface between CONDOR and XFLOS. This interface is configured
via a configuration text file: ``optim.cfg''. I will now
describe the content of ``optim.cfg''.
is an
external code (an executable program): XFLOS. I developed a simple
interface between CONDOR and XFLOS. This interface is configured
via a configuration text file: ``optim.cfg''. I will now
describe the content of ``optim.cfg''.
- Parameter 1:
The filename of the executable that must be launched to run XFLOS.
- Parameters 2 & 3:
The information exchange between CONDOR and XFLOS is based on
files written on the hard drive. There are two files: The first
one is a file written by CONDOR to tell XFLOS what's the current
point we want to evaluate. The second one is written by XFLOS and
is the result of the evaluation. Parameters 2 & 3 are the name of
these files.
- Parameters 4:
Dimension of the search space (31)
- Parameters 5,6 & 7:
The result of a run of XFLOS is a vector of 20 values which must
be aggregated into one single value which is the value of the
objective function at the current point. The aggregation is based
on Parameters 5,6 & 7.
- Parameter 8:
In the industry, there are two kinds of impellers:
- 2D impellers
- 3D impellers
The 2D
impellers are simpler to manufacture and are thus cheaper. The set
of parameters describing a 2D impeller is a subset (9 parameters)
of the 31 parameters needed to describe a 3D impeller. When
optimizing a 2D impeller we must fix 22 parameters and only
optimize 9 parameters. Config-file-Parameter 8 sets the variables
to optimize (=active variable) and those which must be fixed.
Let's define
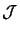 , the set of active variables.
, the set of active variables.
Warning ! If you want, for example, to optimize 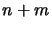 variables, never do the following:
variables, never do the following:
- Activate the first
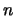 variables, let the
other
variables, let the
other 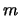 variables fixed, and run CONDOR (Choose as starting
point the best point known so far)
variables fixed, and run CONDOR (Choose as starting
point the best point known so far)
- Activate the second set of
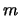 variables, let the first set of
variables, let the first set of 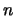 variables fixed, and run
CONDOR (Choose as starting point the best point known so far).
variables fixed, and run
CONDOR (Choose as starting point the best point known so far).
- If the stopping criteria is met then stop, otherwise go back
to step 1.
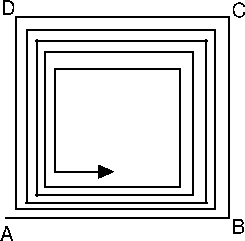
This algorithm is really bad. It will results in a
very slow linear speed of convergence as illustrated in Figure
11.4. The config-file-parameter 8 allows you to
activate/deactivate some variables, it's sometime a useful tool
but don't abuse from it! Use with care!
Figure 11.4:
Illustration of the slow
linear convergence when performing consecutive optimization runs
with some variables deactivated.
 |
- Parameter 9:
Starting point 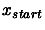 .
.
- Parameter 10:
If some runs of XFLOS have already been computed and saved on the
hard drive, it's possible to tell CONDOR to use the old
evaluations (warm start). If a warm start is
performed, the evaluations needed to build the first quadratic
will be lowered. Beside, it may be interesting to use as starting
point the best point known so far, instead of value specified at
parameter 9. Parameter 10 tells to CONDOR which alternative it
must use for the choice of the starting point.
- Parameter 11:
Lower bound on 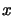 :
: 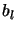
- Parameter 12:
Upper bound on 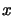 :
: 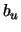
- Parameter 13:
Number 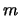 of linear inequalities
of linear inequalities
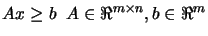 for constrained optimization.
for constrained optimization.
- Parameter 14:
The linear inequalities are described here. Each line represents a
constraint. On each line, you will find:
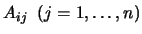 and
and 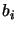 . Using parameter 7, we can let some
variables fixed. In this case, some linear constraints may:
. Using parameter 7, we can let some
variables fixed. In this case, some linear constraints may:
- be simply removed:
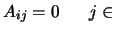
 (
(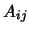 is zero for all the active variables)
is zero for all the active variables)
(
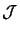 is defined using config-file-parameter 8).
is defined using config-file-parameter 8).
- be removed
and replaced by a tighter bound on the variable
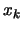 (
(
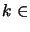
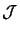 )
)
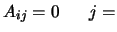
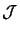
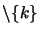 and
and
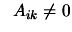 .
.
The 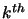 component of
component of 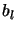 or
or 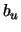 will maybe be updated.
will maybe be updated.
This simple elimination of some linear constraints is implemented
inside CONDOR. It is called in the literature the ``pre-solve
phase''.
- Parameter 15:
The normalization factor for each variables (see Section
12.3 about normalization).
- Parameter 16:
The stopping criteria:
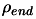 . This criteria is tested inside the normalized space.
. This criteria is tested inside the normalized space.
- Parameter 17:
We consider that the evaluation of the objective function inside
XFLOS has failed when the result of this evaluation is greater
than parameter 17. It means that a ``virtual constraint'' has been
encountered. See Section 12.2.2 for more
information.
- Parameter 18:
In the method project, some constraints are non-linear and have
been hard-coded inside the class ``METHODObjectiveFunction''.
Parameter 18 activates/deactivates these non-linear constraints.
- Parameter 19:
This parameter is the name of the file which contains all the
evaluations of the objective function already performed. This file
can be used to warm start (see parameter 10).
- Parameter 20:
When XFLOS is running, CONDOR is waiting. CONDOR regularly checks
the hard drive to see if the result file of XFLOS has appeared.
Parameter 20 defines the time interval between two successive
checks.
Here is a simple example of a ``server configuration file'':
; number of CPU's (not used currently)
;1
; IP's (not used currently)
;127.0.0.1
; blackbox objective function
;/home/andromeda_2/fld_user/METHOD/TD21/splitter
/home/fvandenb/L6/splitter
;testoptim
; objective function: input file:
/home/fvandenb/L6/000/optim.out
; objective function: output file:
/home/fvandenb/L6/000/xflos.out
; number of input variables (x vector) for the objective function
31
; The objective function is ofunction= sum_over_i ( w_i * ( O_i - C_i)^(e_i) )
; of many variables. The weights (w_i) are:
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 20 0 -1 20
; C_i are:
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0956 0 0 0.521
; e_i are:
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
; optimization of only a part of the variables:
;dz zh1 rh2 zs1 rs2 sleh sles sh1 sh2 th1 th3 ss1 ss2 ts0 ts1 ts3 tkh tks b0 b2 r2 r0 delt bet2 str coel dle el11 el12 el21 el22
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1
; a priori estimated x (starting point)-
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
; 21 22 23 24 25 26 27 28 29 30 31
; dz zh1 rh2 zs1 rs2 sleh sles sh1 sh2 th1 th3 ss1 ss2 ts0 ts1 ts3 tkh tks b0 b2 r2
; r0 delt bet2 str coel dle el11 el12 el21 el22
0.1068 0.0010 0.055555 0.0801 0.2245 0.0096 0.000 0.3 0.37 -0.974 -1.117010721 0.297361 0.693842 -0.301069296 -0.8 -1.117010721 0.004 0.0051 0.07647 0.035 0.225 0.07223 0.0 -0.99398 0.00 4.998956 0.000 0.000 0.000 0.000 0.0000
; use previous line as starting point:
; - 1: yes
; - 0: no, use best point found in database.
1
; lower bounds for x
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
;dz zh1 rh2 zs1 rs2 sleh sles sh1 sh2 th1 th3 ss1 ss2 ts0 ts1 ts3 tkh tks b0 b2 r2 r0 delt bet2 str coel dle el11 el12 el21 el22
0 0 0 0 0 0 0 0 0 -1.7 -1.7 0 0 -1.7 -1.7 -1.7 .002 .002 0 0 0 .05 0 -1.0 -.5 0.1 -0.05 0 0 0 0
; upper bounds for x
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
;dz zh1 rh2 zs1 rs2 sleh sles sh1 sh2 th1 th3 ss1 ss2 ts0 ts1 ts3 tkh tks b0 b2 r2 r0 delt bet2 str coel dle el11 el12 el21 el22
1 1 2 1 2 1 1 1 1 1.7 1.7 1 1 1.7 1.7 1.7 .05 .05 2 1 2 1 2 -0.4 .5 10 0.05 0.02 0.02 0.02 0.02
; number of inequalities
15
;0
; here would be the matrix for inequalities definition if they were needed
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
;dz zh1 rh2 zs1 rs2 sleh sles sh1 sh2 th1 th3 ss1 ss2 ts0 ts1 ts3 tkh tks b0 b2 r2 r0 delt bet2 str coel dle el11 el12 el21 el22 RHS
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 .35
0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 .35
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1 1 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 1 0
; scaling factor for the normalization of the variables.
; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
; dz zh1 rh2 zs1 rs2 sleh sles sh1 sh2 th1 th3 ss1 ss2 ts0 ts1 ts3 tkh tks b0 b2 r2 r0 delt bet2 str coel dle el11 el12 el21 el22
1e-3 1e-3 1e-3 1e-3 1e-3 1e-3 1e-3 1e-2 1e-2 1e-2 1e-2 1e-2 1e-2 1e-2 1e-2 1e-2 5e-4 5e-4 1e-3 1e-3 1e-3 1e-3 1e-3 1e-2 1e-3 1e-2 1e-3 1e-3 1e-3 1e-3 1e-3
; stopping criteria \rho_end=
1e-4
;1e-8
; bad value of the objective function
3
; Nuovo Pignone non-linear constaints hard coded into code must be
; - activated : 1
; - desactivated: 0
;1
1
; the data are inside a file called:
;/home/andromeda_2/fld_user/METHOD/TD21/data.ll
/home/fvandenb/L6/dataNEW.ll
; when waiting for the result of the evaluation of the objective
; function, we check every xxx seconds for an arrival of the file
; containing the results
3
When running CONDOR inside a cluster of computers (to do parallel
optimization), the user must start on each client-node the
CONDOR-client-software. This software is performing the following:
- Wait to receive from the server a sampling site (a point)
(using nearly no CPU time).
- Evaluate the objective function at this site and return
immediately the result to the server. Go to step 1.
Each client node will use a different ``client configuration
file''. These files contain simply the parameters 1 to 7 of the
''server configuration file'' (described in Section
11.4). The IP addresses and the port numbers of
the client nodes are currently still hard coded inside the code
(at the beginning of
file ``parallel.cpp'').



Next: Conclusions
Up: The METHOD project
Previous: Preliminary numerical results
Contents
Frank Vanden Berghen
2004-04-19