| The optimum. We search for it. | |
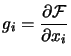 |
|
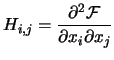 |
|
|
|
The Hessian Matrix of F at point |
|
|
The current approximation of the Hessian Matrix of F at point
If not stated explicitly, we will always assume |
|
|
The Hessian Matrix at the optimum point. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (2.1) |
| (2.2) |
| linear convergence |
|
| superlinear convergence |
|
| quadratic convergence |
|
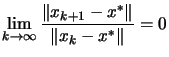 |
(2.3) |
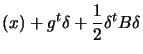
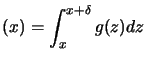
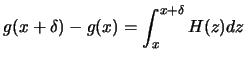
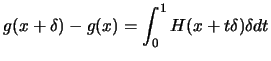
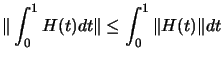 , and the cauchy-swartz inequality
, and the cauchy-swartz inequality
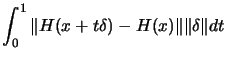 |
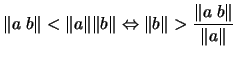 with
with
![$\displaystyle \Vert g(v)-g(u) \Vert \geq \Bigg[ \frac{1}{\Vert H(x)^{-1} \Vert} -
\frac{\gamma}{2} (\Vert v-x\Vert+\Vert u-x\Vert) \Bigg] \Vert v-u\Vert $](img169.png)
![$\displaystyle \Vert g(v)-g(u) \Vert \geq \Bigg[ \frac{1}{\Vert H(x)^{-1} \Vert} - \gamma
\epsilon \Bigg] \Vert v-u\Vert $](img171.png)
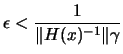 the lemma is proven with
the lemma is proven with
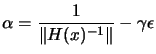 .
.
| 0 | |||
| 0 | |||
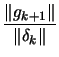 |
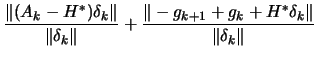 |
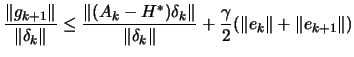
| 0 | 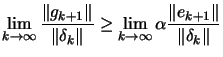 |
||
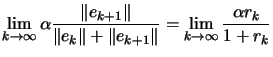 |
(2.12) |
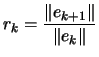 . This implies that:
. This implies that:
| (2.13) |
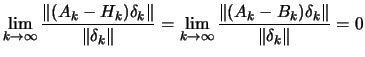 |
(2.14) |