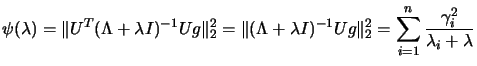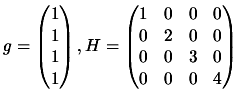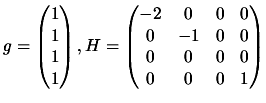


Next: Finding the root of
Up: The Trust-Region subproblem
Previous: must be positive definite.
Contents
Subsections
Theorem 2 tells us that we should be looking for solutions to
4.9 and implicitly tells us what value of 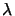 we
need. Suppose that
we
need. Suppose that 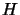 has an eigendecomposition:
has an eigendecomposition:
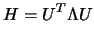 |
(4.8) |
where 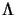 is a diagonal matrix of eigenvalues
is a diagonal matrix of eigenvalues
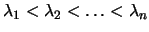 and
and 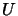 is an
orthonormal matrix of associated eigenvectors. Then
is an
orthonormal matrix of associated eigenvectors. Then
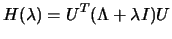 |
(4.9) |
We deduce immediately
from Theorem 2 that the value of 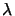 we seek must satisfy
we seek must satisfy
![$ \lambda^* > \min [ 0, -\lambda_1 ]$](img577.png) (as only then is
(as only then is
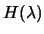 positive semidefinite) (
positive semidefinite) (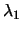 is the least eigenvalue of
is the least eigenvalue of
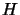 ). We can compute a solution
). We can compute a solution
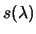 for a given value of
for a given value of
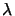 using:
using:
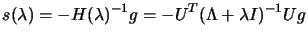 |
(4.10) |
The solution we are looking for
depends on the non-linear inequality
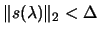 . To say more we need to examine
. To say more we need to examine
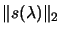 in detail.
For convenience we define
in detail.
For convenience we define
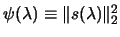 . We have that:
. We have that:
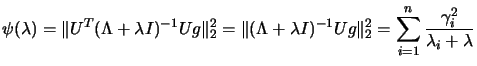 |
(4.11) |
where
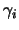 is
is ![$ [Ug]_i$](img585.png) , the
, the 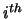 component of
component of 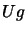 .
.
Suppose the problem is defined by:
We plot
the function
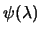 in Figure 4.1. Note the
pole of
in Figure 4.1. Note the
pole of
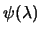 at the negatives of each eigenvalues of
at the negatives of each eigenvalues of
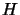 . In view of theorem 2, we are only interested in
. In view of theorem 2, we are only interested in
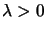 . If
. If 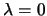 , the optimum lies inside the trust region
boundary. Looking at the figure, we obtain
, the optimum lies inside the trust region
boundary. Looking at the figure, we obtain
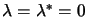 ,
for
,
for
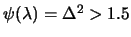 . So, it means that if
. So, it means that if
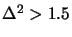 , we have an internal optimum which can be computed
using 4.9. If
, we have an internal optimum which can be computed
using 4.9. If
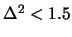 , there is a unique value of
, there is a unique value of
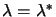 (given in the figure and by
(given in the figure and by
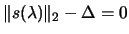 |
(4.12) |
which, used inside
4.9, give the optimal 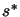 .
.
Figure 4.1:
A plot of
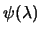 for
for 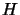 positive
definite.
positive
definite.
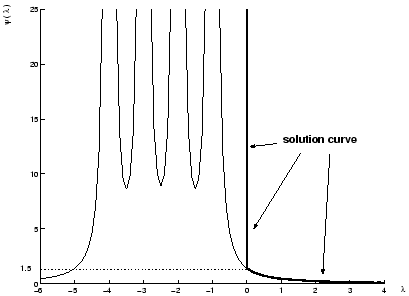 |
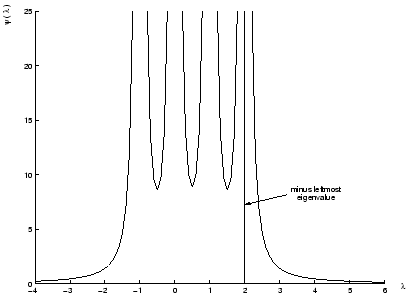
Suppose the problem is defined by:
We plot
the function
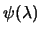 in Figure 4.2. Recall that
in Figure 4.2. Recall that
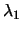 is defined as the least eigenvalue of
is defined as the least eigenvalue of 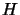 . We are only
interested in values of
. We are only
interested in values of
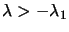 , that is
, that is
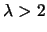 . For value of
. For value of
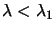 , we have
, we have
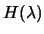 NOT
positive definite. This is forbidden due to theorem 2. We can see
that for any value of
NOT
positive definite. This is forbidden due to theorem 2. We can see
that for any value of 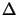 , there is a corresponding value of
, there is a corresponding value of
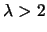 . Geometrically, H is indefinite, so the model function
is unbounded from below. Thus the solution lies on the
trust-region boundary. For a given
. Geometrically, H is indefinite, so the model function
is unbounded from below. Thus the solution lies on the
trust-region boundary. For a given 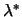 , found using
4.14, we obtain the optimal
, found using
4.14, we obtain the optimal 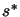 using 4.9.
using 4.9.
Figure 4.2:
A plot of
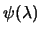 for
for  indefinite.
indefinite.
 |
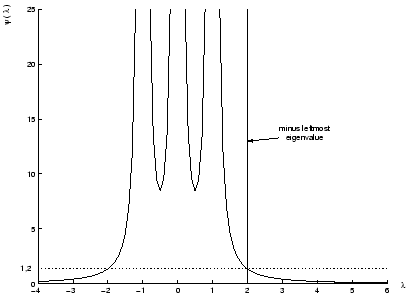
Suppose the problem is defined by:
We plot
the function
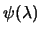 in Figure 4.3. Again,
in Figure 4.3. Again,
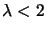 , is forbidden due to theorem 2. If,
, is forbidden due to theorem 2. If,
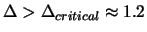 , there is no acceptable value of
, there is no acceptable value of
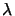 . This difficulty can only arise when
. This difficulty can only arise when 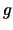 is orthogonal
to the space
is orthogonal
to the space 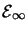 , of eigenvectors corresponding to the most
negative eigenvalue of
, of eigenvectors corresponding to the most
negative eigenvalue of 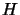 . When
. When
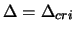 , then
equation 4.9 has a limiting solution
, then
equation 4.9 has a limiting solution 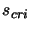 , where
, where
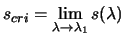 .
.
Figure 4.3:
A plot of
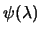 for
for 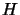 semi-definite and singular(hard case).
semi-definite and singular(hard case).
 |
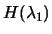 is positive semi-definite and singular and
therefore 4.9 has several solutions. In particular, if
is positive semi-definite and singular and
therefore 4.9 has several solutions. In particular, if
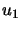 is an eigenvector corresponding to
is an eigenvector corresponding to 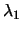 , we have
, we have
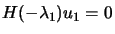 , and thus:
, and thus:
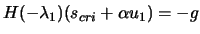 |
(4.13) |
holds for any value of the
scalar 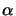 . The value of
. The value of 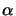 can be chosen so that
can be chosen so that
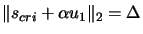 . There are two roots to this
equation:
. There are two roots to this
equation: 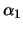 and
and 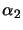 . We evaluate the model at
these two points and choose as solution
. We evaluate the model at
these two points and choose as solution
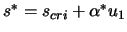 , the lowest one.
, the lowest one.



Next: Finding the root of
Up: The Trust-Region subproblem
Previous: must be positive definite.
Contents
Frank Vanden Berghen
2004-04-19