


Next: Termination Test.
Up: The Trust-Region subproblem
Previous: How to find a
Contents
The Rayleigh quotient trick
If 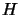 is symmetric and the vector
is symmetric and the vector 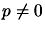 , then the scalar
is known as
the Rayleigh quotient of p. The Rayleigh quotient is
important because it has the following property:
, then the scalar
is known as
the Rayleigh quotient of p. The Rayleigh quotient is
important because it has the following property:
![$\displaystyle \lambda_{min}[H] \leq \frac{\langle p, H p\rangle}{\langle
p,p\rangle} \leq \lambda_{max}[H]$](img683.png) |
(4.21) |
During the Cholesky factorization of
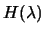 , we have
encountered a negative pivot at the
, we have
encountered a negative pivot at the
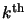 stage of the
decomposition for some
stage of the
decomposition for some 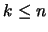 . The factorization has thus
failed (
. The factorization has thus
failed (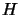 is indefinite). It is then possible to add
is indefinite). It is then possible to add
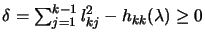 to the
to the
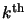 diagonal of
diagonal of
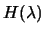 so that the leading
so that the leading 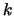 by
by 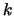 submatrix of
is
singular. It's also easy to find a vector
submatrix of
is
singular. It's also easy to find a vector 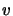 for which
for which
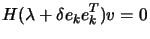 |
(4.22) |
using the
Cholesky factors accumulated up to step 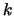 . Setting
. Setting 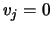 for
for
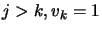 , and back-solving:
gives the
required vector. We then obtain a lower bound on
, and back-solving:
gives the
required vector. We then obtain a lower bound on
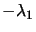 by
forming the inner product of 4.24 with
by
forming the inner product of 4.24 with 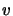 , using the
identity
, using the
identity
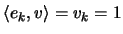 and recalling that the
Rayleigh quotient is greater then
and recalling that the
Rayleigh quotient is greater then
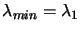 , we
can write:
This implies the bound on
, we
can write:
This implies the bound on 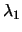 :
In the
algorithm, we set
:
In the
algorithm, we set
![$ \displaystyle \lambda_L = \max [ \lambda_L,
\lambda + \frac{\delta}{ \Vert v\Vert _2^2 } ]$](img696.png)



Next: Termination Test.
Up: The Trust-Region subproblem
Previous: How to find a
Contents
Frank Vanden Berghen
2004-04-19
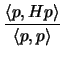
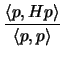
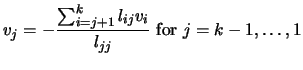
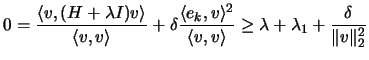
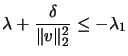
![$ \displaystyle \lambda_L = \max [ \lambda_L,
\lambda + \frac{\delta}{ \Vert v\Vert _2^2 } ]$](img696.png)