


Next: Generating and from and
Up: The secondary Trust-Region subproblem
Previous: The secondary Trust-Region subproblem
Contents
Let us define 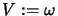 ,
,
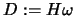 ,
,
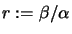 ,
equation 5.8, can now be rewritten:
,
equation 5.8, can now be rewritten:
We will now search for 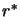 , root of the Equation
, root of the Equation
(Using the fact that
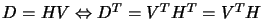 .)
.)
We thus obtain a simple equation
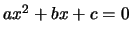 . We find the two
roots of this equation and choose the one
. We find the two
roots of this equation and choose the one 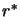 which maximize
5.8.
which maximize
5.8. 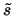 is thus
is thus 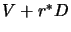 .
.
Frank Vanden Berghen
2004-04-19
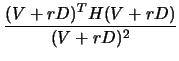
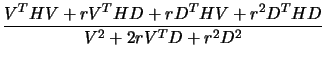
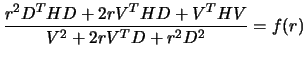
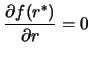
![$\displaystyle \quad \bigg[ (D^T H D) (V^T D) - D^2 D^2 \bigg]
r^2 + \bigg[ (D^T H D) V^2 - D^2 (V^T D) \bigg] r + \bigg[ D^2 V^2
- (V^T D)^2 \bigg]=0$](img778.png)