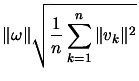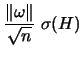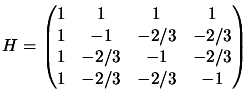


Next: Generating .
Up: Unconstrained Optimization
Previous: An estimation of the
Contents
The secondary Trust-Region subproblem
The material of this chapter is based on the following reference:
[Pow00].
We seek an approximation to the solution 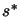 , of the
maximization problem:
, of the
maximization problem:
The following maximization problem is equivalent (after a
translation) and will be discussed in the chapter:
We will indifferently use the term, polynomial, quadratic or
model. The ``trust region'' is defined by the set of all points
which respect the constraint
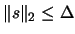 .
.
Further, the shape of the trust region allows 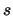 to be replaced
by
to be replaced
by 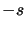 , it's thus equivalent to consider the computation
, it's thus equivalent to consider the computation
Now, if 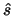 and
and 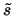 are the values that maximize
are the values that maximize
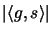 and
and
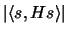 ,
respectively, subject to
,
respectively, subject to
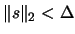 , then
, then 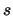 may be an
adequate solution of the problem 5.1, if it is the
choice between
may be an
adequate solution of the problem 5.1, if it is the
choice between
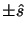 and
and
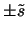 that gives the
largest value of the objective function of the problem. Indeed,
for every feasible
that gives the
largest value of the objective function of the problem. Indeed,
for every feasible 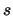 , including the exact solution of the
present computation, we find the elementary bound
, including the exact solution of the
present computation, we find the elementary bound
It follows that the proposed choice of 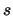 gives a
value of
gives a
value of 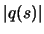 that is, at least, half of the optimal value.
Now,
that is, at least, half of the optimal value.
Now, 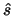 is the vector
is the vector
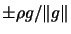 , while
, while 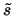 is an eigenvector of an eigenvalue of
is an eigenvector of an eigenvalue of 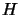 of largest modulus,
which would be too expensive to compute. We will now discuss how
to generate
of largest modulus,
which would be too expensive to compute. We will now discuss how
to generate 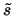 . We will use a method inspired by the
power method for obtaining large eigenvalues.
. We will use a method inspired by the
power method for obtaining large eigenvalues.
Because
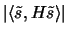 is large only
if
is large only
if
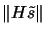 is substantial, the technique begins by
finding a column of
is substantial, the technique begins by
finding a column of 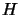 ,
, 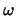 say, that has the greatest
Euclidean norm. Hence letting
say, that has the greatest
Euclidean norm. Hence letting
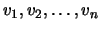 be the columns
of the symmetric matrix
be the columns
of the symmetric matrix 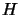 , we deduce the bound
, we deduce the bound
Where
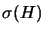 is the spectral
radius of
is the spectral
radius of 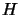 . It may be disastrous, however to set
. It may be disastrous, however to set 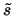 to
a multiple of
to
a multiple of 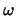 , because
, because
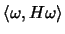 is zero in the case:
is zero in the case:
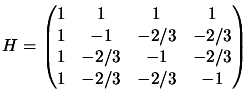 |
(5.6) |
Therefore, the algorithm picks
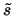 from the two dimensional linear subspace of
from the two dimensional linear subspace of 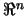 that is spanned by
that is spanned by 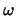 and
and 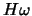 . Specifically,
. Specifically,
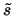 has the form
has the form
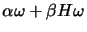 , where
the ratio
, where
the ratio
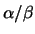 is computed to maximize the expression
is computed to maximize the expression
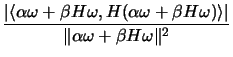 |
(5.7) |
which determines the direction of
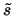 . Then the length of
. Then the length of 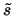 is defined by
is defined by
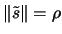 , the sign of
, the sign of 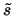 , being unimportant.
, being unimportant.
Subsections



Next: Generating .
Up: Unconstrained Optimization
Previous: An estimation of the
Contents
Frank Vanden Berghen
2004-04-19
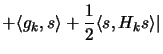
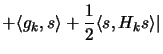
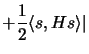
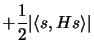
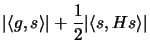
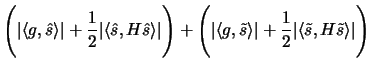
![$\displaystyle 2 \max\Bigg[ \vert \langle g, \hat{s} \rangle \vert + \frac{1}{2}...
...le \vert + \frac{1}{2} \vert \langle \tilde{s}, H
\tilde{s}\rangle \vert \Bigg]$](img749.png)