


Next: Noisy optimization
Up: Numerical Results of CONDOR.
Previous: Hock and Schittkowski set
Contents
Parallel results on the Hock and Schittkowski set
We are using the same test conditions as in the previous section
(standard objective functions with standard starting points).
Since the objective function is assumed to be time-expensive to
evaluate, we can neglect the time spent inside the optimizer and
inside the network transmissions. To be able to make this last
assumption (negligible network transmissions times), a wait loop
of 1 second is embedded inside the code used to evaluate the
objective function (only 1 second: to be in the worst case
possible).
Figure 7.2:
Improvement due to parallelism
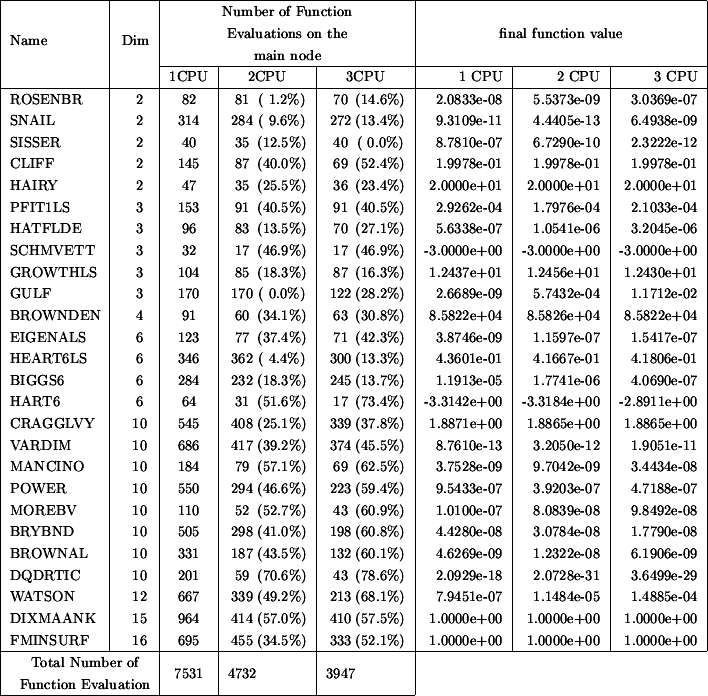 |
Table 7.2 indicates the number of function evaluations
performed on the master CPU (to obtain approximatively the total number of function
evaluations cumulated over the master and all the slaves, multiply the given number
on the list by the number of CPU's). The CPU time is thus directly proportional
to the numbers listed in columns 3 to 5 of the Table 7.2.
Suppose a function evaluation takes 1 hour. The parallel/second
process on the main computer has asked 59 minutes ago to a client
to perform one such evaluation. We are at step 4(a)i of the main
algorithm. We see that there are no new evaluation available from
the client computers. Should we go directly to step 4(a)ii and use
later this new information, or wait 1 minute? The response is
clear: wait a little. This bad situation occurs very often in our
test examples since every function evaluation takes exactly the
same time (1 second). But what's the best strategy when the
objective function is computing, randomly, from 40 to 80 minutes
at each evaluation (this is for instance the case for objective
functions which are calculated using CFD techniques)? The response
is still to investigate. Currently, the implemented strategy is:
never wait. Despite, this simple strategy, the current algorithm
gives already some non-negligible improvements.



Next: Noisy optimization
Up: Numerical Results of CONDOR.
Previous: Hock and Schittkowski set
Contents
Frank Vanden Berghen
2004-04-19
