

Next: Starting and safe-guarding Newton's
Up: The Trust-Region subproblem
Previous: Explanation of the Hard
Contents
We will apply the 1D-optimization algorithm called ``1D Newton's
search'' (see Annexes, Section 13.5) to the
secular equation:
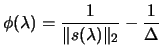 |
(4.14) |
We use the secular equation instead of
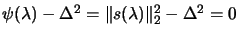 inside the ``1D Newton's
search'' because this last function is better behaved than
inside the ``1D Newton's
search'' because this last function is better behaved than
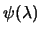 . In particular
. In particular
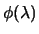 is strictly
increasing when
is strictly
increasing when
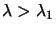 , and concave. It's first
derivative is:
, and concave. It's first
derivative is:
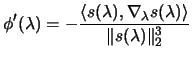 |
(4.15) |
where
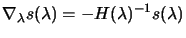 |
(4.16) |
The
proof of these properties will be skipped.
In order to apply the ``1D Newton's search'':
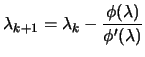 |
(4.17) |
we need to evaluate the function
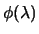 and
and
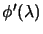 . The value of
. The value of
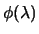 can be obtained by
solving the Equation 4.9 to obtain
can be obtained by
solving the Equation 4.9 to obtain
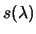 . The
value of
. The
value of
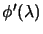 is available from 4.17 once
is available from 4.17 once
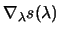 has been found using 4.18.
Thus both values may be found by solving linear systems involving
has been found using 4.18.
Thus both values may be found by solving linear systems involving
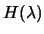 . Fortunately, in the range of interest,
. Fortunately, in the range of interest,
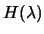 is definite positive, and thus, we may use its Cholesky factors
is definite positive, and thus, we may use its Cholesky factors
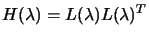 (see Annexes, Section
13.7 for notes about Cholesky decomposition ). Notice that
we do not actually need tho find
(see Annexes, Section
13.7 for notes about Cholesky decomposition ). Notice that
we do not actually need tho find
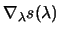 , but
merely the numerator
, but
merely the numerator
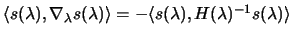 of 4.17. The simple relationship
of 4.17. The simple relationship
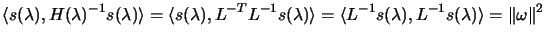 |
(4.18) |
explains
why we compute 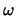 in step 3 of the following algorithm. Step
4 of the algorithm follows directly from 4.17 and
4.19. Newton's method to solve
in step 3 of the following algorithm. Step
4 of the algorithm follows directly from 4.17 and
4.19. Newton's method to solve
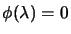 :
:
- find a value of
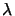 such that
such that
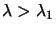 and
and
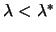 .
.
- factorize
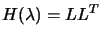
- solve
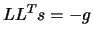
- Solve
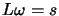
-
Replace 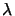 by by 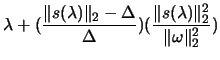 |
(4.19) |
- If stopping criteria are not met, go to step 2.
Once the algorithm has reached point 2. It will always generate
values of
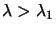 . Therefore, the Cholesky
decomposition will never fails and the algorithm will finally find
. Therefore, the Cholesky
decomposition will never fails and the algorithm will finally find
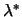 . We skip the proof of this property.
. We skip the proof of this property.



Next: Starting and safe-guarding Newton's
Up: The Trust-Region subproblem
Previous: Explanation of the Hard
Contents
Frank Vanden Berghen
2004-04-19