

Next: 1D Newton's search
Up: Annexes
Previous: Notions of constrained optimization
Contents
The secant equation
Let us define a general polynomial of degree 2:
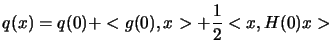 |
(13.27) |
where
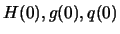 are constant. From the rule for differentiating a
product, it can be verified that:
if
are constant. From the rule for differentiating a
product, it can be verified that:
if 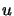 and
and 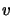 depend on
depend on 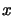 . It therefore
follows from 13.27 (using
. It therefore
follows from 13.27 (using
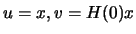 ) that
) that
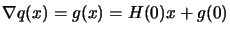 |
(13.28) |
A consequence of 13.28 is that if 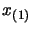 and
and
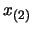 are two given points and if
are two given points and if
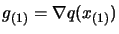 and
and
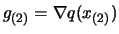 (we simplify the notation
(we simplify the notation
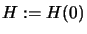 ), then
), then
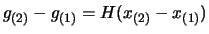 |
(13.29) |
This is called the ``Secant
Equation''. That is the Hessian matrix maps the differences in
position into differences in gradient.
Frank Vanden Berghen
2004-04-19