


Next: How to pick inside
Up: The Trust-Region subproblem
Previous: Finding the root of
Contents
In step 1 of Newton's method, we need to find a value of 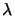 such that
such that
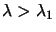 and
and
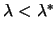 . What
happens if
. What
happens if
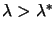 (or equivalently
(or equivalently
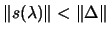 )? The Cholesky factorization succeeds and so we can
apply 4.21. We get a new value for
)? The Cholesky factorization succeeds and so we can
apply 4.21. We get a new value for 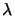 but we must
be careful because this new value can be in
the forbidden region
but we must
be careful because this new value can be in
the forbidden region
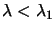 .
.
If we are in the hard case, it's never possible to get
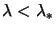 (or equivalently
(or equivalently
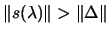 ),
therefore we will never reach point 2 of the Newton's method.
),
therefore we will never reach point 2 of the Newton's method.
In the two cases described in the two previous paragraphs, the
Newton's algorithm fails. We will now describe a modified Newton's
algorithm which prevents these failures:
- Compute
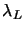 and
and 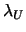 respectively a lower and
upper bound on the lowest eigenvalue
respectively a lower and
upper bound on the lowest eigenvalue 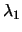 of
of 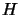 .
.
- Choose
![$ \lambda \in [\lambda_L \lambda_U]$](img643.png) . We will choose:
. We will choose:
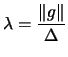
- Try to factorize
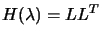 (if not already done).
(if not already done).
- Success:
- solve
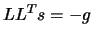
- Compute
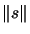 :
:
-
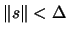 :
:
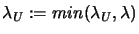
We must be careful: the next value of 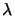 can be in the
forbidden
can be in the
forbidden
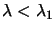 region. We may also have interior
convergence: Check
region. We may also have interior
convergence: Check 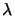 :
:
-
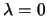 : The algorithm is finished. We have found the
solution
: The algorithm is finished. We have found the
solution 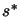 (which is inside the trust region).
(which is inside the trust region).
-
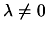 : We are maybe in the hard case. Use the
methods described in the paragraph containing the Equation
4.15 to find
: We are maybe in the hard case. Use the
methods described in the paragraph containing the Equation
4.15 to find
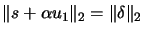 . Check
for termination for the hard case.
. Check
for termination for the hard case.
-
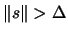 :
:
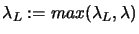
- Check for termination for the normal case:
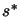 is on the
boundary of the trust region.
is on the
boundary of the trust region.
- Solve
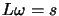
- Compute
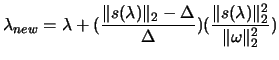
- Check
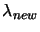 : Try to factorize
: Try to factorize
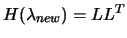
- Success: replace
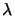 by
by
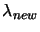
- Failure:
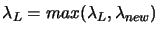
The Newton's method, just failed to choose a correct 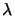 .
Use the ``alternative'' algorithm: pick
.
Use the ``alternative'' algorithm: pick 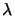 inside
inside
![$ [\lambda _L \lambda _U]$](img14.png) (see Section 4.5 ).
(see Section 4.5 ).
- Failure: Improve
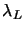 using Rayleigh's quotient
trick (see Section 4.8 ). Use the ``alternative''
algorithm: pick
using Rayleigh's quotient
trick (see Section 4.8 ). Use the ``alternative''
algorithm: pick  inside
inside
![$ [\lambda _L \lambda _U]$](img14.png) (see
section 4.5 ).
(see
section 4.5 ).
- return to step 3.



Next: How to pick inside
Up: The Trust-Region subproblem
Previous: Finding the root of
Contents
Frank Vanden Berghen
2004-04-19
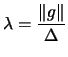
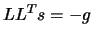
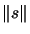 :
:
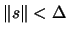 :
:
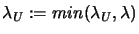
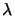 can be in the
forbidden
can be in the
forbidden
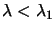 region. We may also have interior
convergence: Check
region. We may also have interior
convergence: Check 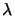 :
:
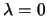 : The algorithm is finished. We have found the
solution
: The algorithm is finished. We have found the
solution 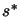 (which is inside the trust region).
(which is inside the trust region).
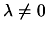 : We are maybe in the hard case. Use the
methods described in the paragraph containing the Equation
4.15 to find
: We are maybe in the hard case. Use the
methods described in the paragraph containing the Equation
4.15 to find
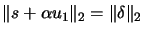 . Check
for termination for the hard case.
. Check
for termination for the hard case.
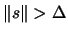 :
:
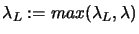
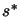 is on the
boundary of the trust region.
is on the
boundary of the trust region.
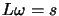
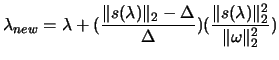
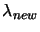 : Try to factorize
: Try to factorize
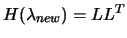
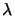 by
by
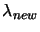
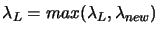
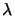 .
Use the ``alternative'' algorithm: pick
.
Use the ``alternative'' algorithm: pick 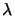 inside
inside
![$ [\lambda _L \lambda _U]$](img14.png) (see Section 4.5 ).
(see Section 4.5 ).
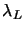 using Rayleigh's quotient
trick (see Section 4.8 ). Use the ``alternative''
algorithm: pick
using Rayleigh's quotient
trick (see Section 4.8 ). Use the ``alternative''
algorithm: pick 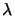 inside
inside
![$ [\lambda _L \lambda _U]$](img14.png) (see
section 4.5 ).
(see
section 4.5 ).