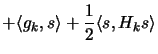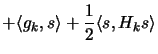


Next: Linear constraints
Up: Constrained Optimization
Previous: Constrained Optimization
Contents
A short review of the available techniques.
In the industry, the objective function is very often a simulator
of a complex process. The constraints usually represents bounds on
the validity of the simulator. Sometimes the simulator can simply
crash when evaluating an infeasible point (a point which do not
respects the constraints). For this reason, the optimization
algorithm generates only feasible points (due to rounding errors,
some points may be infeasible especially when there are non-linear
constraints. Anyway, the generated infeasible points are always
very close to feasibility ).
There are two possible approaches. The first approach is now
described.
The steps 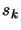 of the unconstrained algorithm are the solution
of:
of the unconstrained algorithm are the solution
of:
In the first approach (=``approach 1"), the step 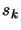 of
the constrained algorithm are the solution of:
of
the constrained algorithm are the solution of:
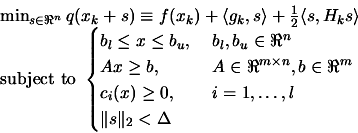 |
(8.2) |
The problem of solving 8.2 is not trivial at all. It's
in fact as difficult as the original problem. The only advantage
in solving this subproblem at each step is that the objective
function (which is 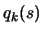 ) evaluations are cheap and thus we can
have very precise steps leading (hopefully) to a fast convergence
to the solution of the original problem.
) evaluations are cheap and thus we can
have very precise steps leading (hopefully) to a fast convergence
to the solution of the original problem.
The same methods used for solving the subproblem 8.2
can be directly applied to the original non-linear objective
function. This is our second approach (=``approach 2").
There are specific methods for box or linear constraints and for
non-linear constraints. We will describe them in two separate
chapters.
Subsections



Next: Linear constraints
Up: Constrained Optimization
Previous: Constrained Optimization
Contents
Frank Vanden Berghen
2004-04-19